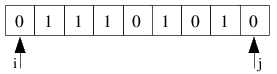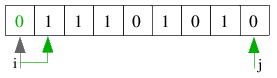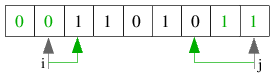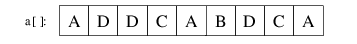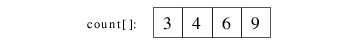5. Radixsort
[ Zurück zum Inhaltsverzeichnis ]
5.1 Hintergrund
Die Sortierverfahren, welche wir in den bisherigen Kapiteln kennen gelernt haben, stützen sich allesamt auf
Schlüsselvergleiche zum Sortieren der Daten, d.h. die Schlüssel als Ganzes werden miteinander verglichen und
bei Bedarf getauscht. Die Sortierverfahren, die jetzt behandelt werden sollen, nutzen hingegen die
arithmetischen Eigenschaften der Schlüssel aus. Dabei wird angenommen, dass es sich bei den Schlüsseln um
Wörter aus einem m-adischen Alphabet handelt (z.B. m=10 für Dezimalzahlen, m=2 für Dualzahlen, m=26
für Wörter über dem lateinischen Alphabet), man die Schlüssel also als m-adische Zahlen auffassen kann.
Daher nennt man m auch die Wurzel (engl./lat.: radix) der Schlüsseldarstellung und die
darauf aufbauenden Sortieralgorithmen Radixsort-Verfahren.
Diese betrachten die einzelnen Stellen der m-adischen Schlüssel. Bei Dezimalzahlen würde also jede Ziffer,
bei Dualzahlen jedes Bit und bei Zeichenketten jedes Zeichen zum Sortieren heran gezogen werden und nicht
wie bei anderen Sortierverfahren die Schlüssel an sich. Daher bezeichnet man die Radixsort's auch als
digitale Sortieralgorithmen.
Anwendung finden die Radixsort-Verfahren z.B. dort, wo nur nach bestimmten Schlüsselstellen sortiert werden
soll - hier wären andere Sortiermethoden machtlos. Anders bei Radixsort: eine mögliche Variante wäre es, eine
Bitmaske zu erstellen, die an denjenigen Schlüsselstellen, nach denen sortiert werden soll, eine 1 hat und
dann nur diese Stellen in die Sortierung einzubeziehen.
Die hier vorgestellten Verfahren sollen der Einfachheit halber wie in der Computertechnik üblich auf das
duale Zahlensystem zurückgreifen, also die einzelnen Bits als Schlüsselstellen betrachten und darauf ihre
Sortierungen aufbauen. Dies ist auch sinnvoll, da eigentlich alles, was in einem Digitalrechner dargestellt
wird, in Binärzahlen umgewandelt werden kann und moderne Programmiersprachen einfache Operatoren und
Möglichkeiten bereitstellen, um auf die einzelnen Binärziffern einer Variablen zugreifen zu können.
Zunächst soll in diesem Kapitel auf Radix Exchange Sort eingegangen werden, welches Quicksort sehr
ähnelt, die Schlüssel von links nach rechts bitweise betrachtet und sukzessive nach 0/1 in 2 Gruppen
unterteilt, wodurch eine endgültige Sortierung erreicht wird.
Als Zwischenschritt soll dann eine Erläuterung von Bucketsort erfolgen, welches
verstanden werden muss für das darauf aufbauende Straight Radix Sort sowie ein lineares Verfahren
als Verallgemeinerung dieser digitalen Sortiermethode.
5.2 Bit-Operationen
Da sich die hier vorgestellten Sortierverfahren auf Vergleiche von Bitstellen stützen, ist es unersetzlich,
einzelne bzw. mehrere Bits aus einem Schlüssel extrahieren zu können.
Die Programmiersprache C stellt dafür einige Operatoren bereit: mit x<<y und x>>y werden die Bits
der Variablen x um y Stellen nach links bzw. rechts verschoben, x&y verknüpft x bitweise UND mit y - dies
genügt uns schon, um die beiden benötigten Funktionen zu definieren.
Die erste Funktion getbit() wird von Radix Exchange Sort und Straight Radix Sort verwendet, um
den Wert eines Bits an einer bestimmten Stelle zurückzuliefern:
inline unsigned getbit(unsigned x, int k){ return (x>>k)&1; }
k gibt dabei die von rechts gesehene Stelle an, für welche der Bitwert geliefert werden soll,
getbit(x,0) würde z.B. den Wert des am weitesten rechts gelegenen Bits zurückgeben.
Die Verallgemeinerung von Straight Radix Sort mit Bucketsort greift auf die folgende Funktion
getbits() zurück, welche den Wert mehrerer Bits zurück liefert:
inline unsigned getbits(unsigned x, int k, int j){ return (x>>k)&~(~0<<j); }
Diese Funktion liefert die j Bits zurück, die k Bits von rechts in x angeordnet sind.
Kurz zur Erläuterung: ~(~0<<j) stellt eine Maske dar, die aus Einsen auf den am weitesten rechts
stehenden j Bitstellen und Nullen auf den übrigen Positionen besteht. Eine logische UND-Verknüpfung dieser
Maske mit dem um k Bits nach rechts verschobenen Schlüssel führt dann dazu, dass duch die Nullen in der Maske
diese Bits auf jeden Fall 0 sind und die j rechten Bits durch die Einsen in der Maske den Wert des
verschobenen Schlüssels erhalten und zurück geliefert werden.
Folgendes Bild illustriert einen Aufruf von getbits() für den gegebenen Schlüssel. k=3 und j=2, sodass die
2 Bits zurück gegeben werden, welche 3 Bits von rechts im Schlüssel angeordnet sind.

5.3 Radix Exchange Sort
Bei diesem, auch als digitales Austausch-Sortierverfahren bekannten Algorithmus, werden die Bits in den
Schlüsseln sukzessive von links nach rechts betrachtet. Es ist leicht ersichtlich, dass alle Schlüssel mit
führender 0 kleiner sind als Schlüssel mit führender 1. Die Schlüssel werden demnach so umgeordnet, dass
zunächst die gesamte Datei betrachtet und nach der am weitesten links stehenden Bitstelle sortiert wird.
Das heißt, die Datei wird in 2 Gruppen unterteilt: die linke Gruppe enthält alle Schlüssel, deren gerade
betrachtete Bitstelle 0 ist, die rechte enthält die Schlüssel mit den 1-Bits. Rekursiv werden diese beiden
Gruppen nun nach dem gleichen Algorithmus geteilt, wobei pro Rekursionsschicht immer die nächste Bitstelle
betrachtet wird. Die Rekursion erfolgt solange, bis entweder alle Bitstellen betrachtet wurden oder aber alle
Gruppen nur noch aus einem Element bestehen - die Folge gilt dann als eindeutig sortiert.
Radix Exchange Sort ist deutlich erkennbar als "Teile-und-Herrsche"-Algorithmus und kommt dem ebenfalls auf
diesem Prinzip beruhenden Quicksort sehr nahe. Wie bei Quicksort wird die Datei erst in 2 Gruppen geteilt,
was aus der Verwendung von binären Schlüsselstellen resultiert (2 Gruppen für 0- und 1-Bits).
Daraufhin erfolgen getrennt für die linke und rechte Teildatei die beiden rekursiven Aufrufe.
Und so ist die programmiertechnische Realisierung auch erfreulich ähnlich zu der von Quicksort.
Wie bei diesem wird das Feld mit zwei Zeigern durchlaufen, die Ganzzahlen auf Arrayindizes darstellen.
Der linke Zeiger startet beim linken Rand der Folge nach rechts und hält an, wenn ein Schlüssel gefunden wird,
dessen gerade betrachtetes Bit 1 ist. Der rechte Zeiger steht zu Beginn auf dem Ende der Folge und durchläuft
diese nach links, bis ein Schlüssel mit einem 0-Bit an der entsprechenden Bitstelle gefunden wird. In diesem
Fall werden die Elemente von linkem und rechtem Zeiger miteinander vertauscht. Diese Prozedur läuft solange,
bis beide Zeiger aufeinander treffen und hat zur Folge, dass jetzt in der linken Teildatei nur Elemente mit
0-Bits und in der rechten Datei nur Elemente mit 1-Bits an der relevanten Bitstelle enthalten sind. Im
Gegensatz zu Quicksort, bei dem das Trennelement willkürlich gewählt werden konnte, handelt es sich bei diesem
digitalen Sortierverfahren stets um die Zahl 2b, wenn b die soeben betrachtete Bitstelle ist.
Da nicht gesagt ist, dass diese Zahl in der Schlüsselfolge enthalten ist, kann es auch keine Garantie dafür
geben, dass wie bei Quicksort durch einen rekursiven Aufruf ein Element seinen endgültigen Platz in der Datei
erhält und nicht weiter betrachtet werden muss.
Durch die Ähnlichkeiten mit Quicksort ist es auch nicht verwunderlich, dass der zugehörige Code frapierende
Übereinstimmungen aufweist. Hier eine mögliche Variante, deren Aufruf mit radixexchange(a,0,n-1,8*sizeof(int));
für n Elemente und Ganzzahlen (int's) als Schlüssel erfolgt:
inline unsigned getbit(unsigned x, int k){ return (x>>k)&;1; }
void radixexchange(int a[], int l, int r, int b){ //b=von rechts zu betrachtende Bitstelle
b--;
int t, i, j;
if(r>l && b>=0){ //Dateilänge>1 && noch Bitstellen übrig?
i=l; j=r; //i=linker Rand, j=rechter Rand
while(j!=i){ //solange linker nicht rechter Zeiger
while(getbit(a[i],b)==0 && i<j) i++; //halte an, wenn 0 von links gefunden
while(getbit(a[j],b)!=0 && j>i) j--; //halte an, wenn 1 von rechts gefunden
t=a[i]; a[i]=a[j]; a[j]=t; //tausche beide Elemente
}
if(getbit(a[r],b)==0) j++; //wenn Datei komplett aus 0 bestehend
radixexchange(a,l,j-1,b); //Aufruf für linke Teildatei
radixexchange(a,j,r,b); //Aufruf für rechte Teildatei
}
}
Wieder ein paar Worte zur Erklärung des Codes: in der Parameterliste gibt b die von rechts aus gesehene
zu betrachende Bitstelle der momentan zwischen l und r befindlichen Datei an. Der Code wird nur ausgeführt,
wenn die Länge der aktuellen Datei größer 1 ist und wenn das eben betrachtete Bit nicht aus der Folge rechts
herausläuft. Dann werden die beiden Zeiger auf den linken und rechten Rand der Folge gesetzt und die
Schleife betreten, die ein Aufteilen in die beiden Teildateien bewirkt. Hier wird zunächst der linke Zeiger
solange inkrementiert, bis er auf eine 1 stößt oder auf den rechten Zeiger trifft. Im Gegensatz zu Quicksort
ist der zusätzliche Zeigertest hier nötig, da nur ein Bit untersucht wird und man sich nicht auf Marken verlassen
kann, um das Durchsuchen mit den Zeigern abzubrechen. Das Gleiche gilt für die zweite innere Schleife, die
dann stoppt, wenn ein 0-Bit von rechts gefunden wurde. Sollte dies geschehen sein, so werden die beiden
Elemente miteinander vertauscht. Dies ist auch der Fall, wenn die inneren Schleifen aufgrund eines
Aufeinandertreffens der beiden Zeiger verlassen worden sind - tut aber nichts zur Sache, in diesem Fall würde
nur das Element, bei welchem die Zeiger aufeinander getroffen sind, mit sich selber vertauscht werden, was
keine Auswirkungen hat. Sollten die beiden Zeiger auf dem selben Element stehen, so ist eine Teilung der Datei
fast abgeschlossen. Links stehen jetzt alle Elemente mit 0 im b-ten Bit, rechts alle Elemente mit einer 1 an
der selbigen Stelle. Das Element a[i] ist jetzt das am weitesten links stehende aus der rechten Teildatei, hat
also eine 1 an der b-ten Bitstelle. Dies gilt nicht, wenn die Datei an dieser Bitstelle komplett aus Nullen
bestanden hat. Der Test direkt nach der äußeren Schleife berücksichtigt diesen Fall und setzt j eine Position
weiter, um den ersten rekursiven Aufruf die gesamte Datei berücksichtigen zu lassen.
Da die Datei jetzt geteilt ist, muss die Spaltung nur noch abgeschlossen werden, indem wie bei Quicksort die
Rekursionen erfolgen. Kehren diese zurück, so gilt die aktuelle Teildatei als sortiert.
Folgendes Beispiel verdeutlicht einen Durchlauf der Funktion ohne die rekursiven Aufrufe. Dargestellt ist die
jeweils b-te Bitstelle der 9 vorhandenen Schlüssel.
| 1.) Die Ausgangssituation: zu sehen ist das jeweils b-te Bit eines Schlüssels, die beiden Zeiger i und j sind schon initialisiert und zeigen auf den linken sowie rechten Rand der Folge. |
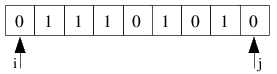 |
| 2.1) i findet eine 1 auf der nächsten Position, j steht beteits auf einer 0. Die beiden Schleifen brechen
deswegen ab und die beiden Schlüssel werden miteinander vertauscht. |
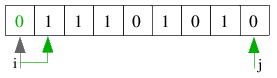 |
| 2.2) Eine Position weiter findet i wieder eine 1 vor, j muss zwei Positionen nach links gerückt werden,
bis es eine 0 vorfindet. Die beiden Elemente werden vertauscht und die Zeiger rücken weiter. |
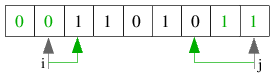 |
| 2.3) Wieder muss i nur eine Position weiter und j zwei Positionen zurück gesetzt werden. Nach dem
anschließenden Tausch ist die Sortierung der Datei nach dieser Bitstelle fast abgeschlossen. |
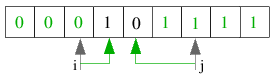 |
| 3.) i wird noch eine Position weiter gesetzt und verharrt dort, da das darauf stehende Bit eine 1 ist.
j hat dieselbe Position wie i, wodurch die entsprechende Schleife sofort abbricht. Nach dem harmlosen Tausch
des Elementes mit sich selbst wird die äußere Schleife beendet und die Datei ist nach dieser Bitstelle
sortiert. |
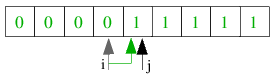 |
Nachfolgend noch ein kurzes Beispiel, wie ein Testdatenfeld durch den Algorithmus durchlaufen und dabei
sortiert wird.
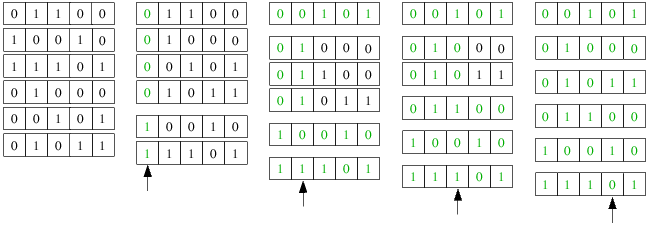
Grüne Bitstellen bedeuten, dass diese vom Algorithmus nicht mehr betrachtet werden. Größere Abstände zwischen
den Testdatensätzen sollen die rekursive Abspaltung in 2 Gruppen verdeutlichen. Der Pfeil unter einem Bild
soll das derzeit betrachtete Bit b darstellen.
Das erste Bild zeigt die Ausgangssituation: die 6 Datensätze, deren Schlüssel aus je 5 Bits bestehen, liegen
unsortiert vor.
Im zweiten Bild wird das erste Bit betrachtet und die Daten so umverteilt, dass 2 Gruppen mit 0- und 1-Bits
an dieser ersten Dualziffer entstehen.
Im dritten Bild werden die beiden entstandenen Gruppen getrennt voneinander nach dem 2. Bit von links
sortiert. In der ersten Gruppe gibt es gleich eine Abspaltung von einem Element, da dieses das einzige mit
einer 0 an dieser Bitstelle ist. Dieses wird aus der weiteren Betrachtung ausgeschlossen, da es eindeutig
an seiner endgültigen Position eingeordnet wurde. Auch die zweite Teildatei aus dem vorherigen Bild kann in
diesem Schritt eindeutig sortiert werden, da sie aus nur zwei Elementen bestand und diese an der 2. Bitstelle
unterschiedliche Werte haben.
In Bild vier werden die 3 übrig gebliebenen Elemente sortiert. Dabei kommt es wieder zu einer eindeutigen
Abspaltung eines Elementes und somit bleiben nur noch 2 zu betrachtende Schlüssel übrig.
Das fünfte Bild zeigt die eindeutige Einordnung der letzten zwei Elemente, da die sich in der 4. Bitstelle
unterscheiden. Da alle Elemente einen eindeutigen Platz in der Folge bekommen konnten, kann diese nun als
sortiert angesehen werden, wozu noch nicht einmal alle Bitstellen betrachtet werden mussten.
Noch ein paar Gedanken zur Effizienz von Radix Exchange Sort: idealerweise würde natürlich wie bei Quicksort
eine Datei genau in der Mitte in 2 Teildateien getrennt werden. Das Problem ist, dass durch den Algorithmus
auch führende Nullen mit betrachtet werden und diese machen oftmals den halben Schlüssel aus. Erst in den
niederwertigeren Bits entscheidet sich dann die endgültige Sortierung der Datei - so kommt es auch häufig vor,
dass bei den hohen Bits nur kleine Teildateien abgesprengt werden und somit der Algorithmus nicht effizient
arbeiten kann. Laufzeithemmend kommt hinzu, dass bei gleichen Schlüsseln alle Bits dieser Schlüssel betrachtet
werden, was zusätzlichen Rechenaufwand erfordert - daher funktioniert Radix Exchange Sort für Dateien mit
vielen gleichen Schlüsseln nicht gut. Bei zufälligen Bits in den Schlüsseln arbeitet der Algorithmus
allerdings ähnlich gut wie Quicksort, welches hingegen besser an weniger zufällige Situationen
angepasst werden kann und im Allgemeinen trotzdem schneller ist.
Zu guter Letzt bleibt noch zu erwähnen, dass sich Radix Exchange Sort genauso wie Quicksort verbessern lässt,
indem z.B. die Rekursion beseitigt wird oder kleine Teildateien mittels Insertion Sort behandelt werden.
5.4 Bucketsort
Als Zwischenschritt will ich hier eine stabile Sortiermethode betrachten, die wir für die nachfolgend
dargestellten Sortierverfahren benötigen, welche aber nicht auf der binären Darstellung von Schlüsseln beruht.
Beim Bucketsort (auch distribution counting/Verteilungszählen oder Sortieren durch
Fachverteilung genannt) handelt es sich sogar um einen quasi linearen Sortieralgorithmus, wobei man aufpassen
muss, da linear nicht unbedingt heißt, dass es auch schneller arbeitet als z.B. Quicksort.
Effizient funktioniert dieses Verfahren vor allem dann, wenn eine Datei vorliegt, in der die Anzahl
unterschiedlicher Schlüssel begrenzt ist, d.h. viele identische Schlüssel vorliegen. Wenn bei n Datensätzen
M unterschiedliche Schlüssel existieren und M hinreichend klein ist, kann man Bucketsort anwenden, welches
in diesem Fall effektiver ist als z.B. Quicksort.
Die Idee besteht darin, dass man zunächst die Datei durchläuft, um die Anzahl der Schlüssel zu jedem
der M Werte zu ermitteln. Das Ergebnis dieser Zählung speichert man in einem Array count[], welches natürlich
M Elemente aufnehmen muss und dann bei einem zweiten Durchlauf durch die Datei verwendet wird, um die endgültigen
Positionen der Schlüssel in der sortierten Datei zu bestimmen und diese in einem Hilfsarray b[] (welches von
gleicher Dimension wie das zu sortierende Array a[] sein muss) abzuspeichern. Anschließend muss aus b zurück nach
a kopiert werden, will man das Ergebnis hier stehen haben.
Folgender Codeausschnitt realisiert genau das:
for(j=0; j<M; j++) count[j]=0; //count[] mit 0 initialisieren
for(i=0; i<N; i++) count[a[i]]++; //Vorkommen der Schlüssel speichern
for(j=1; j<M; j++)
count[j]=count[j-1]+count[j]; //Positionen im Array bestimmen
for(i=N-1; i>=0; i--)
b[--count[a[i]]]=a[i]; //in b einordnen, jeweiligen Zähler verringern
for(i=0; i<N; i++) a[i]=b[i]; //auf a zurück speichern
Die erste for-Schleife initialisiert count[] mit 0, in der zweiten for-Schleife erfolgt der erste Durchlauf durch
die Datei, wobei die Anzahl der M verschiedenen Schlüssel gezählt und in count[] gespeichert wird. Diese werden
in der dritten for-Schleife aufaddiert, um somit die Startpositionen gleicher Schlüssel im sortierten Array
festzulegen. In der vierten Schleife erfolgt die eigentliche sortierte Einordnung im Hilfsspeicher b und zu guter
Letzt die Rückspeicherung nach a.
Um die Verfahrensweise dieses Einordnens deutlicher zu machen, soll folgendes Beispiel verwendet werden:
| 1.) Ausgangssituation: wir haben N=9 Schlüssel, wobei es nur M=4 unterschiedliche Werte gibt. Eigentlich müssten
diese 0-4 heißen, zur besseren Verdeutlichung wurden sich jedoch mit A, B, C und D benannt. |
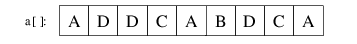 |
| 2.1) Die zweite for-Schleife obigen Codes zählt die Vorkommen der einzelnen Schlüssel und speichert sie in
count[]. count[] ist von der Dimension M=4 und kann somit alle Vorkommen unterschiedlicher Werte speichern. |
 |
| 2.2) count[] enthält nun die Anzahl der einzelnen Werte. A ist 3-mal, B 1-mal, C 2-mal und D 3-mal vorhanden.
Mit der 3. for-Schleife werden benachbarte count-Werte addiert. |
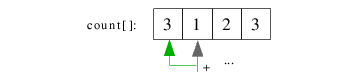 |
| 2.3) Durch die Addition ergibt sich folgendes count[]-Feld. Die einzelnen Werte zeigen jetzt im sortierten Array
auf eine Position nach dem letzten Vorkommen des damit verbundenen Schlüssels. So ist count[0]=3, der dazu gehörende
Schlüssel A kommt 3-mal vor, muss also auf a[0], a[1] und a[2] abgespeichert werden. a[count[0]]=a[3] zeigt somit auf
das Element hinter dem letzten Vorkommen von A im sortierten Feld. |
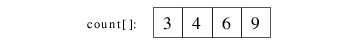 |
| 3.1) Nun wird die Datei zum zweiten Mal durchlaufen. Unter b[] ist noch einmal illustriert, auf welchen Elementen
die count[]-Zeiger stehen. Dieser Durchlauf erfolgt von hinten nach vorn, wobei jedes Element i genommen und an seine
Position count[a[i]]-1 im sortierten Array eingeordnet wird. Hier wird z.B. das letzte Element A genommen,
count['A']=count[0]=3, sodass A an seine Position count[0]-1=2 eingeordnet wird. |
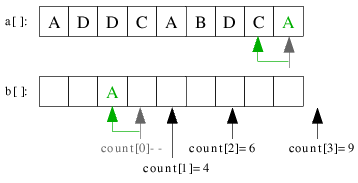 |
| 3.2) Der nächste Schlüssel C wird auf seine Position count['C']-1=count[3]-1=5 eingeordnet. |
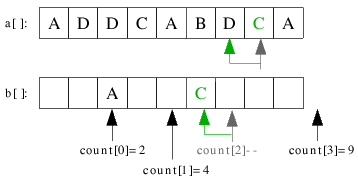 |
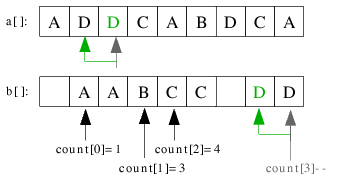
| 3.3) D wird auf der letzten Position eingeordnet und count[3] dekrementiert. |
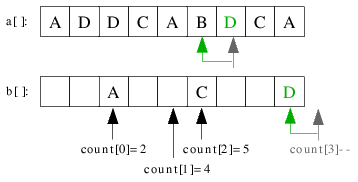 |
| 3.4) Das einzige B in der Folge wird an seine Stelle count[2]-1 eingeordnet. |
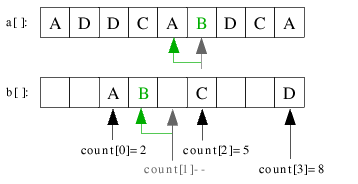 |
| 3.5) Das nächste A kommt auf seine Position count[0]-1=1. |
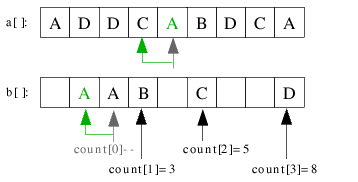 |
| 3.6) Das zweite C wird links vom ersten C auf Position count[2]-1=4 kopiert. |
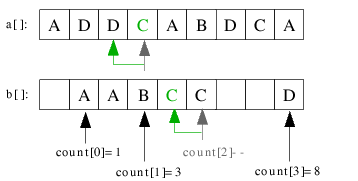 |
| 3.7) count[3] wird dekrementiert und D an die entsprechende Stelle im Hilfsarray b[] einsortiert. |
 |
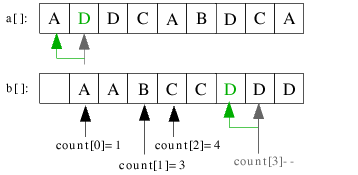
| 3.8) Das nächste D kommt ebenso auf seine Position. |
 |
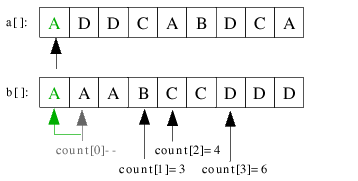
| 3.9) Der letzte fehlende Schlüssel A wird auf die letzte leere Stelle kopiert und die Datei gilt als sortiert. |
 |
Das war doch nicht schwer, oder? Schön lässt sich auch erkennen, dass die relative Sortiertheit der einzelnen gleichen
Schlüssel erhalten bleibt, da der zweite Durchlauf durch die Datei "von hinten nach vorn" stattfindet. D.h. hätte man
die einzelnen A's usw. indiziert mit A1, A2... dann würde diese Reihenfolge auch in der sortierten
Datei erhalten bleiben. Dies ist wichtig, da das gleich besprochene Straight Radix Sort davon ausgeht, dass diese
Stabilität gegeben ist.
Man könnte sich fragen, warum nicht gezählt wird und dann die einzelnen Schlüssel gleich ohne weitere Betrachtung in das
Array einsortiert werden. Man müsste nur den Wert von Schlüssel i kennen und könnte ihn gleich count[i]-mal in das Array
schreiben und schon hätte man nach Abarbeitung für alle Schlüssel ein sortiertes Feld. Das kann man bei einstelligen
Schlüsseln ruhig machen, Bucketsort findet aber vor allem dort Anwendung, wo die Schlüssel aus mehreren Ziffern bestehen.
Z.B. könnte man Dezimalzahlen haben und mit Bucketsort von rechts nach links nach allen Dezimalziffern sortieren lassen,
um am Ende ein sortiertes Feld zu haben. Da nur immer in 10 Fächer (für jede der 10 Ziffern 0-9, also M=10) eingeordnet
werden muss, ist der zusätzliche Speicheraufwand für count[] auch überschaubar und Bucketsort arbeitet ausreichend
schnell. Es muss also davon ausgegangen werden, dass es sich bei dem Wert nur um einen Teil des eigentlichen Schlüssels
handelt und dann der ganze Schlüssel an seine Stelle im Array kopiert werden muss.
Übrigens: ist M=2, so gleicht die eben beschriebene Vorgehensweise dem Straight Radix Sort, auf welches gleich noch
ausführlicher eingegangen werden soll.
5.5 Straight Radix Sort
Dieses Verfahren, auch geradliniges digitales Sortieren genannt, betrachtet die einzelnen Schlüsselbits
im Gegensatz zu Radix Exchange Sort von rechts nach links. Dabei werden die Schlüssel bei jedem neuen Bit wieder
nach 0 und 1 sortiert, bis alle Bits betrachtet wurden - die Datei gilt als sortiert.
Man muss ein wenig überlegen, um sich von dem Funktionieren dieser Methode zu überzeugen - tatsächlich führt sie
nur dann zum Erfolg, wenn der Prozess des Sortierens nach einem Bit stabil ist. Was das heißt, lässt sich schnell
erklären: vor der Betrachtung des beispielsweise 3. Bits von rechts ist die Datei bei Straight Radix Sort schon
nach den ersten beiden hinteren Bits sortiert. Wird nun nach dem 3. Bit sortiert, so muss die relative
Sortiertheit der beiden hinteren Bits erhalten bleiben. Wenn es z.B. zwei Schlüssel gibt, welche im 3. Bit
gleich sind, dann muss nach der Sortierung nach diesem Bit der Schlüssel, welcher von den hinteren beiden Bits her
kleiner war, immernoch vor dem anderen Schlüssel stehen. Diese Stabilität zu erreichen ist aber nicht schwer, man
kann allerdings z.B. nicht die Teil-Methoden verwenden, wie sie bei Quicksort oder Radix Exchange Sort zur
Anwendung gekommen sind.
Vielmehr können wir die stabile Methode des Bucketsorts verwenden, um diesen Algorithmus zu implementieren. Die Anzahl an
unterschiedlichen Schlüsseln ist dabei M=2 (0 und 1), sodass jeweils in nur 2 Fächer eingeordnet werden muss und sich somit
der zusätzliche Speicherbedarf für count[] auf zwei int-Variablen beschränkt, der Speicherbedarf für das Hilfsfeld b aber
natürlich noch bei n Elementen liegt. Die generelle Vorgehensweise sollte nicht schwer zu verstehen sein: betrachte die
Schlüssel nach ihren Bits für alle Bitstellen von rechts nach links und sortiere nach den einzelnen Bitwerten mit
Bucketsort. Führe dies solange aus, bis alle Bitstellen der Schlüssel betrachtet wurden.
Nach dieser Methode lässt sich Straight Radix Sort wie folgt implementieren:
inline unsigned getbit(unsigned x, int k){ return (x>>k)&;1; }
void straightradix(int a[], int N, int bits){
int i, pass, count[2], b[N];
for(pass=0; pass<bits; pass++){ //die Bits der Reihe nach betrachten
count[0]=0; count[1]=0; //count[] mit 0 initialisieren
for(i=0; i<N; i++) count[getbit(a[i],pass)]++; //Vorkommen der Bits speichern
count[1]+=count[0]; //Position im Array bestimmen
for(i=N-1; i>=0; i--)
b[--count[getbit(a[i],pass)]]=a[i]; //in b einordnen, jeweiligen Zähler verringern
for(i=0; i<N; i++) a[i]=b[i]; //auf a zurück speichern
}
}
Aufgrund des Bekanntseins von M=2 konnte Bucketsort so abgewandelt werden, dass zwei Schleifen weggefallen sind, was noch
ein paar Laufzeitvorteile mit sich bringt. Trotzdem muss man aufpassen: in der derzeitigen Version ist Straight Radix Sort
eigentlich nur eines: lahm. Und zwar genau deswegen, weil es absolut jede Bitstelle betrachtet und nicht wie
etwa Radix Exchange Sort nur soweit, bis ein Element als definitiv eingeordnet gilt. Zudem wird pro Bitstelle die Datei
von Bucketsort zweimal komplett durchlaufen und noch ein drittes Mal zur Rückspeicherung von b[] nach a[]. Dieses Verfahren
liegt in seiner Laufzeit auch noch weit hinter Mergesort zurück und ist somit der langsamste zeitoptimale Sortieralgorithmus.
Allerdings wird im kommenden Abschnitt eine Verallgemeinerung der Funktion angegeben werden, welche in praxi sogar schneller
als Quicksort läuft.
Folgendes kleines Beispiel soll kurz die Arbeitsweise von Straight Radix Sort verdeutlichen:
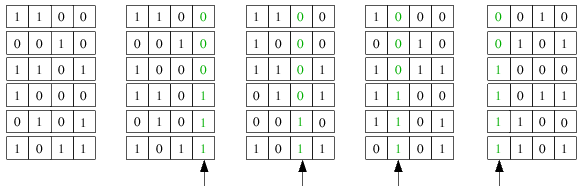
Schön zu sehen ist, dass die Schlüssel bitweise von rechts nach links betrachtet werden und vor allem, dass die Schlüssel bei
jeder Stufe nach den schon betrachteten Bits sortiert sind, was aufgrund des stabilen Bucketsorts möglich ist. Trotzdem ist
dies eine sehr zeitaufwändige Variante, weil die Datei wie schon gesagt ganze dreimal von Bucketsort für jedes Bit betrachtet
werden muss. Eine Abwandlung dieses Algorithmus' wird nachfolgend gegeben.
5.6 Lineares Sortieren
Das beste Ergebnis, auf das man bei einem Sortierverfahren hoffen kann, ist das der Linearität. Was heißt das?:
es bedeutet, dass der Zeitaufwand, der für das Sortieren von n Schlüsseln benötigt wird, linear anwächst, d.h. dass
man sich darauf verlassen kann, dass z.B. bei 2*n Daten sich die Laufzeit verdoppelt, bei 4*n verfierfacht usw. und nicht
wie z.B. bei den elementaren Sortierverfahren mit O(n2) quadriert.
Ein solches lineares Sortierverfahren kann man leicht effektiv durch eine Abwandlung von oben gegebenem Straight Radix Sort
erhalten. Vielmehr verallgemeinert man obige Funktion, wobei die hintergründige Idee ist, dass man statt nur eines
Bits in jedem Durchlauf von Bucketsort gleich m Bits betrachtet, wodurch sich die Anzahl der Fächer, auf die verteilt
wird, von M=2 auf M=2m erhöht. Dies erfordert natürlich wieder das ursprüngliche Bucketsort, da nicht wie
bei M=2 zwei for-Schleifen entfallen können. Außerdem muss zur Extrahierung mehrerer Bits nun die Funktion getbits() verwendet
werden, wie sie oben im Abschnitt 5.2 bereits erläutert wurde. Der Vorteil ist, dass man das Feld nicht
dreimal für jedes einzelne Bit durchlaufen muss, sondern nur für m Bits. Wie man m optimal wählen kann, wird gleich besprochen,
hier erst einmal die verallgemeinerte Funktion von Straight Radix Sort:
inline unsigned getbits(unsigned x, int k, int j){ return (x>>k)&~(~0<<j); }
void linstraightradix(int a[], int N, int bits, int m){
int M=1, i, j, pass, *count, b[N];
if(m<=0 || m>bits/2) m=bits/4; //Fehlerfälle abfangen, auf guten Fall umsetzen
for(i=0; i<m; i++,M*=2); //2^m berechnen
count=(int*)malloc(M*sizeof(int));
for(pass=0; pass<bits/m; pass++){ //die Bits der Reihe nach betrachten
for(j=0; j<M; j++) count[j]=0; //count[] mit 0 initialisieren
for(i=0; i<N; i++) count[getbits(a[i],pass*m,m)]++; //Vorkommen der Schlüssel speichern
for(j=1; j<M; j++)
count[j]=count[j-1]+count[j]; //Positionen im Array bestimmen
for(i=N-1; i>=0; i--)
b[--count[getbits(a[i],pass*m,m)]]=a[i]; //in b einordnen, jeweiligen Zähler verringern
for(i=0; i<N; i++) a[i]=b[i]; //auf a zurück speichern
}
free(count);
}
Folgendes Beispiel soll wieder die Vorgehensweise des Verfahrens verdeutlichen:
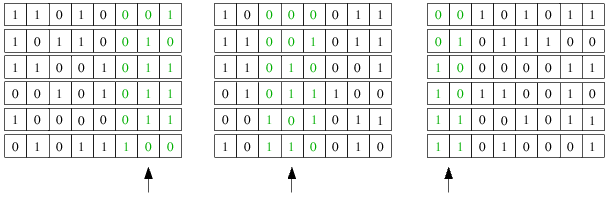
Wie beim ursprünglichen Straight Radix Sort werden die Bits von hinten nach vorn betrachtet, nur dass hier eben nicht nur
ein Bit pro Durchlauf, sondern m Bits gleichzeitig betrachtet werden, sodass nur bits/m Durchläufe durch die äußere Schleife
notwendig sind, um das gegebene Feld zu sortieren. Dadurch wird allerdings auch zusätzlicher Speicher von M=2m
für count[] benötigt. Dieser Speicherbedarf ist nicht zu unterschätzen, heißt es doch, dass bei einer Verdopplung von
m eine Quadrierung von M und somit des zusätzlichen Speicherplatzes erfolgt. Für m=4 sind z.B. nur 16 zusätzliche int's,
für m=16 hingegen schon 65536 Plätze in count[] erforderlich. Noch gravierender fällt natürlich der zusätzliche Platz für
das Feld b[] aus, welches genau soviel Elemente wie a[] aufnehmen muss. Das können bei n=10.000.000 Elementen und
32-Bit-int's schonmal über 38MB sein. Der zusätzlich notwendige Speicher für count[] und vor allem b[] ist auch der
Hauptnachteil dieses linearen Sortierverfahrens. Steht ausreichend Arbeitsspeicher zur Verfügung, stellt das
kaum ein Problem dar, doch zu sortierende Datenbestände sind nicht immer auf Hochleistungsrechnern zu Hause, sodass in
diesem Falle arg abgewogen muss, ob der zusätzliche Speicher bereit gestellt werden kann oder ob man nicht doch lieber
Quicksort verwenden sollte.
Die Frage aller Fragen ist natürlich: wie groß sollte man m wählen, damit das Sortierverfahren optimal arbeitet?
Empirisch habe ich mit einem entsprechenden Programm folgende Zeiten beim Sortieren von 1.000.000 Elementen gemessen:
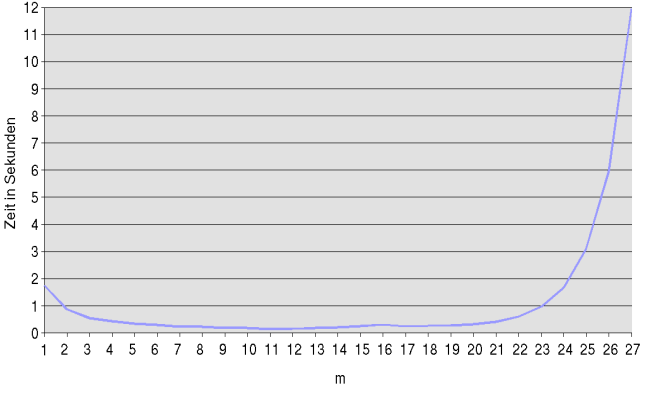
Natürlich muss m zwischen einschließlich 1 und der Anzahl der Bits im Schlüssel liegen. Diese waren hier bei einer normalen
Ganzzahl 32 Bit, allerdings wird schon bei m=28 1GB zusätzlicher Speicher für count[] benötigt, sodass das Programm mit
Speicherzugriffsverletzung abbrach. Offensichtlich ist bei m=11 ein Zeit-Minimum erreicht, auch der zusätzliche Speicher
hält sich mit 2048 int's für count[] (entspricht 8KB) in Grenzen. Allgemein kann man feststellen, dass ungefähr
m=bits/4 zeitoptimal und der Speicheraufwand dabei nicht übermäßig groß ist. Mit dieser Wahl von einem Viertel der
Wortlänge wird die Datei viermal von Bucketsort durchlaufen. Die Schlüssel werden als M-adische Zahlen betrachtet, also zur
Basis M und es gibt insgesamt 4 (M-adische) Ziffern pro Schlüssel.
Da Bucketsort linear arbeitet und dieses verallgemeinerte Straight Radix Sort mit m=bits/4 genau 4 Durchläufe bei
32-Bit-Schlüsseln erfordert, ist das gesamte Verfahren linear. Das ist es auch mit jedem anderen m, so auch das
ursprüngliche Straight Radix Sort, mit m=bits/4 kommt der Geschwindigkeitsvorteil allerdings erst richtig zur Geltung.
Folgende Funktion gibt noch einmal das optimierte Straight Radix Sort mit m=bits/4 an:
inline unsigned getbits(unsigned x, int k, int j){ return (x>>k)&~(~0<<j); }
void linoptstraightradix(int a[], int N, int bits){
int M=1, m, i, j, pass, *count, b[N];
m=bits/4;
for(i=0; i<m; i++,M*=2); //2^m berechnen
count=(int*)malloc(M*sizeof(int));
for(pass=0; pass<bits/m; pass++){ //die Bits der Reihe nach betrachten
for(j=0; j<M; j++) count[j]=0; //count[] mit 0 initialisieren
for(i=0; i<N; i++) count[getbits(a[i],pass*m,m)]++; //Vorkommen der Schlüssel speichern
for(j=1; j<M; j++)
count[j]=count[j-1]+count[j]; //Positionen im Array bestimmen
for(i=N-1; i>=0; i--)
b[--count[getbits(a[i],pass*m,m)]]=a[i]; //in b einordnen, jeweiligen Zähler verringern
for(i=0; i<N; i++) a[i]=b[i]; //auf a zurück speichern
}
free(count);
}
Es hat sich bei mehreren Tests dieses Verfahrens empirisch gezeigt, dass der Geschwindigkeitsvorteil gegenüber einem
verbesserten Quicksort bei zufälligen Permutationen im Bereich von 30-40% liegt.
Trotzdem sollte man mit Bedacht zwischen den einzelnen Sortierverfahren abwägen: gerade wenn man sich bewusst ist, dass
man nicht den meisten Arbeitsspeicher zur Verfügung hat und Millionen von Datensätzen verwalten muss, kann der zusätzliche
Speicherbedarf einer kompletten Kopie des zu sortierenden Feldes zum echten Hindernis werden. Deshalb sollte man vor allem
auf Produktivsystemen mit Bedacht wählen, bevor man sich entscheidet: meist ist ein auch bei weniger Speicher stabil
arbeitendes Quicksort besser als ein schnelleres lineares Sortierverfahren, welches die doppelte Arbeitsspeichermenge
beansprucht. Ein weiterer Aspekt ist die Anpassbarkeit von Quicksort auf wohl definierte Probleme: sind die Eingabedaten
nicht zufällig, so ist bei dem angepassten Straight Radix Sort mit erheblichen Effektivitätsverlusten zu rechnen.
5.7 Laufzeitbetrachtungen
Die Laufzeit der ersten beiden Radix-Sortierverfahren für das Sortieren von n Schlüsseln mit jeweils b Bits
beträgt im Prinzip n*b. Im Wesentlichen bedeutet dies in Abhängigkeit nur von der Variablen n eine Laufzeitkomplexität
von n*log(n), wenn davon ausgegangen wird, dass alle Schlüssel verschieden sind (da b in diesem Fall
wenigstens log(n) sein muss), jedoch werden gewöhnlich viel weniger als n*b Operationen ausgeführt: bei Radix
Exchange Sort, weil es abbricht, wenn ein Schlüssel an einer eindeutigen Position steht, beim verbesserten Straight Radix
Sort, weil hier viele Bits gleichzeitig verarbeitet werden können.
Beide Sortierverfahren benötigen also für das Sortieren von n Schlüsseln mit b Bits weniger als n*b
Bitvergleiche - d.h. in dem Sinne, dass die benötigte Zeit proportional zur Anzahl der Bits in den Schlüsseln
ist, sind die digitalen Sortierverfahren linear - dies folgt auch daraus, dass sich leicht erkennen lässt,
dass jedes Bit höchstens einmal betrachtet wird.
Radix Exchange Sort verwendet im Durchschnitt n*lg(n) Bitvergleiche und ist bei zufälligen Folgen mit Quicksort vergleichbar,
das grundlegende Straight Radix Sort muss wie schon erwähnt ungefähr n*b Bitvergleiche ausführen - da hier jedoch absolut
jedes Bit betrachtet werden muss und das Feld pro Bit dreimal komplett durchlaufen wird, arbeitet es in der Regel sehr
viel langsamer als Radix Exchange Sort oder Quicksort.
Die zuletzt betrachtete lineare Version von Straight Radix Sort mit angepasstem m=bits/4 hingegen kann n Schlüssel in bits/4
Durchläufen sortieren, wobei allerdings zusätzlicher Platz für 2m Zähler und einen Puffer für das Umordnen der
Datei in der Größe dieser benötigt wird, was das größte Hindernis darstellt. Dafür hat man auf einfache Weise ein lineares
Sortierverfahren auf der Hand, welches bei randomisierten Ausgangsfolgen schneller arbeitet als Quicksort und für Aufgaben,
für die genügend Speicherplatz zur Verfügung steht und bei denen es primär auf Geschwindigkeit ankommt, bestens geeignet ist.
[ Zurück zum Inhaltsverzeichnis ]