Fourier-Transformationen bekannter Strukturen
Die Fourier-Transformation stellt ein wichtiges mathematisches Hilfsmittel zur Analyse von Frequenzen aus Signalströmen (z.B. Bildern) dar. Durch sie kann eine beliebige Funktion als Summe verschieden gewichteter Sinus- und Kosinus-Funktionen dargestellt werden. Früher bildete sie in der Bildverarbeitung ein wichtiges Hilfsmittel für die schnelle Anwendung von Filtern durch Multiplikation im Spektralraum, dieser Einfluss hat sich aufgrund steigender Rechnerleistungen immer weiter abgeschwächt. Dass es sich bei der Fourier-Transformation um ein mathematisch elegantes Verfahren handelt, wird am besten bei der Darstellung heraus ragender Strukturen im Spektralraum deutlich. Diese Seite soll einige dieser Strukturen veranschaulichen und daran die Ästhetik der jeweiligen Elemente im Bild- als auch Spektralraum verdeutlichen.
Punktverteilungen
| Ortsraum / Bildraum | Spektralraum / Fourierraum |
| Punktverteilung unter dem Kriterium max. Distanz zu 5 Nachbarpunkten: | |

|

|
| Phyllotaxis - math. Beschreibung des Aufbaus einer Sonnenblumen-Blüte: | |

|
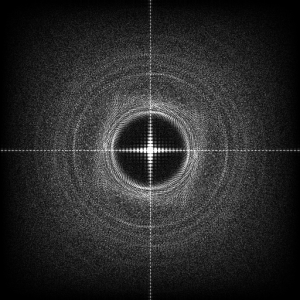
|
Penrose-Parkettierung
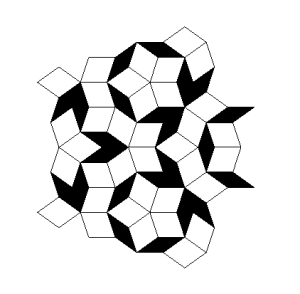
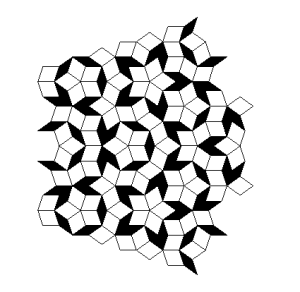
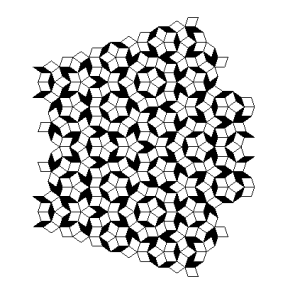
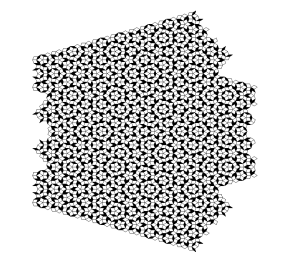
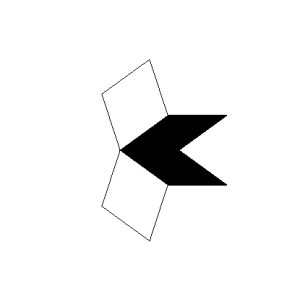
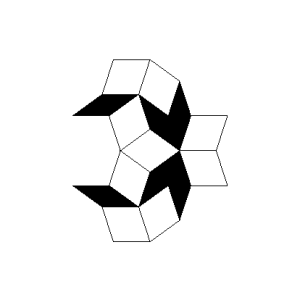
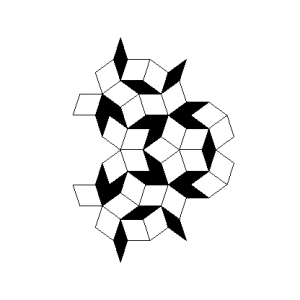
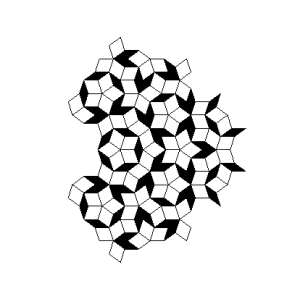
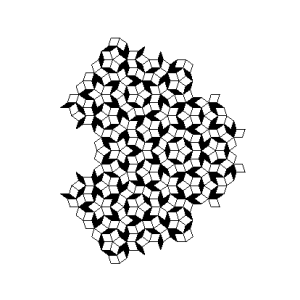
Roger Penrose (geb. 1931), ein englischer Mathematiker und Physiker, publizierte 1974 eine Möglichkeit zur Parkettierung großer Flächen, die sich dadurch auszeichnet, dass sie trotz einer einfachen Struktur und Ästhetik nicht periodisch ist. Ausgehend von 2 Grundelementen (Rhomben) kann rekursiv mittels einfacher Regeln eine immer komplexere Parkettierung erreicht werden, die sich in sich selbst nicht wiederholt.
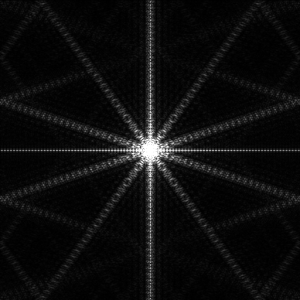
Trotz der Aperiodizität besitzt die Penrose-Parkettierung eindeutige Frequenzen, da durch die Konstruktionsregeln nur bestimmte Drehwinkel für die Grundelemente möglich sind.
| Ortsraum / Bildraum | Spektralraum / Fourierraum |
| Basiselement: Breiter Rhombus | |
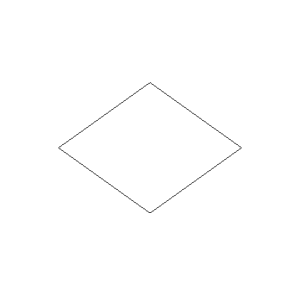
|

|
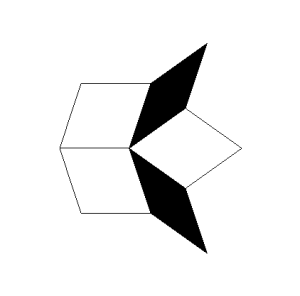
|

|
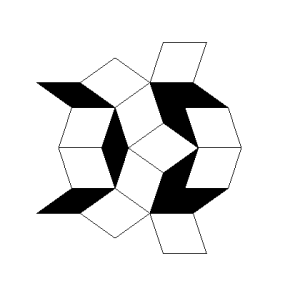
|

|
|

|
|

|
|

|

|

|
|

|

|

|

|

|
| Basiselement: Schmaler Rhombus | |

|

|
|

|
|
|
|

|
|

|
|

|

|

|

|

|

|

|

|

|