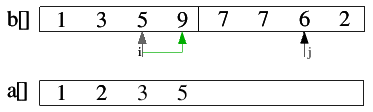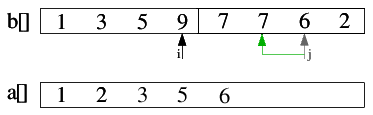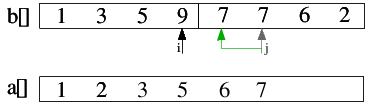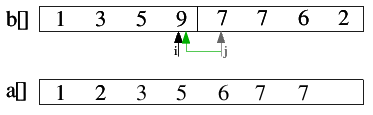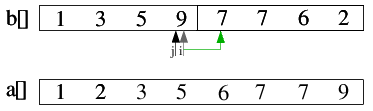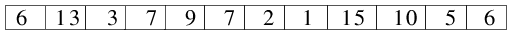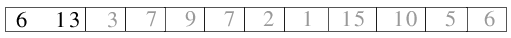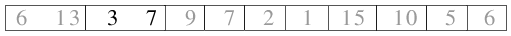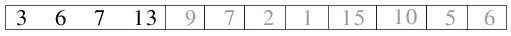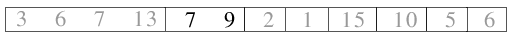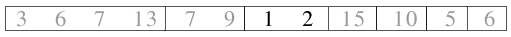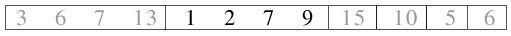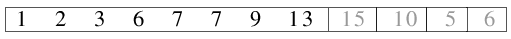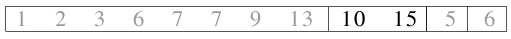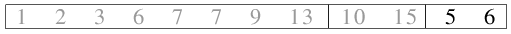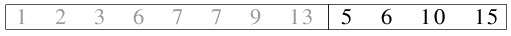3. Mergesort

3.1 Historie/Hintergrund

Mergesort, das "Sortieren durch Verschmelzen", ist eines der ältesten und best-untersuchten Sortierverfahren, welches bereits 1945 von Computerpionier John von Neumann vorgeschlagen und auf dem EDVAC-Computer von ihm implementiert wurde. Im Vergleich zu Quicksort, wo eine Folge rekursiv in 2 Teilfolgen geteilt wurde, findet bei Mergesort ein quasi komplementärer Prozess statt: beim sogenannten Mischen (Merging) werden 2 sortierte Dateien zu einer sortierten Datei zusammen gefügt.
"Teile-und-Herrsche" im Sinne von Quicksort bedeutete: eine Datei wird so umgeordnet, dass sie als sortiert gilt, wenn ihre beiden Teile sortiert sind. Bei Mergesort, welches diesem Prinzip ebenfalls entspricht, bedeutet es hingegen, dass eine Datei in zwei Teile zerlegt wird, die zu sortieren und dann derart zu kombinieren sind, dass sich eine sortierte Gesamtdatei ergibt.
Das Mischen stellt nicht nur einen Konterpart zum Teilen dar, auch ist Mergesort selbst bei rekursiver Implementierung in gewisser Weise ein Komplement zu Quicksort: bei diesem wird zunächst der Teilprozess ausgeführt, gefolgt von den beiden rekursiven Aufrufen für die linke und rechte Teilfolge. Bei Mergesort hingegen werden erst die rekursiven Aufrufe ausgeführt, um anschließend die dadurch entstandenen Teildateien im Mischprozess wieder zu vereinen.
Mergesort bietet einige grundlegende Vorteile gegenüber anderen Sortieralgorithmen: zum einen ist es stabil, d.h. die relative Sortiertheit gleicher Schlüssel in einer Datei bleibt stets erhalten. Zum anderen hat es auch im ungünstigsten Fall eine Laufzeit proportional zu n*log(n), also O(n*log(n)). Weiterer Vorteil: Mergesort kann so implementiert werden, dass es die Daten hauptsächlich sequentiell abarbeitet, was vor allem beim Sortieren auf Externspeicher und von verketteten Listen wichtig ist.
Hauptnachteil: für den Algorithmus wird ein zu n proportionaler zusätzlicher Speicher benötigt - daher wird Mergesort vor allem dort angewandt, wo zusätzlicher Speicherplatz keine Rolle spielt. Zudem ist es oftmals das Verfahren der Wahl, wenn es gilt eine große sortierte Datenmenge zu verwalten und immer wieder Datensätze einzuordnen. Normalerweise würden die neuen Daten angehangen und die komplette Datei neu sortiert werden. Weitaus besser wäre es hingegen, die neuen Daten getrennt zu sortieren und dann mit der bestehenden Datei zu vereinen - ein ideales Szenario für den Mischprozess von Mergesort.

3.2 Der Algorithmus

So wie man bei Quicksort das Prinzip des Teilens verstehen muss, so muss man bei Mergesort den Mischprozess verstehen. Mischen im Sinne von Mergesort bedeutet, dass man zwei sortierte Dateien zu einer einzigen sortierten Datei vereint. Zuerst erfolgt also eine Aufteilung der Gesamtdatei auf Dateien der Länge 1. Nun nimmt man benachbarte Teildateien dieser Länge, die also nur aus einem Element bestehen und trivial als sortiert gelten, und mische (sortiere und kombiniere) sie zu Dateien der Länge 2. Diese nimmt man wiederum und mische sie zu Dateien der Länge 4 usw. bis es nur noch 2 Dateien gibt. Diese werden schlussendlich ebenfalls gemischt, sodass eine einzige Datei entsteht, die der sortierten Ausgangsfolge entspricht.
Diese Art der Kombination zweier Dateien zu einer heißt 2-Wege-Mergesort. Es gibt weiterhin x-Wege-Mergesort-Varianten, welche x Dateien zu einer vereinen - diese sollen hier allerdings nicht weiter betrachtet werden.

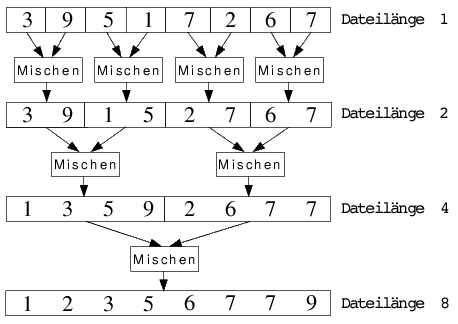
Folgendes kleines Beispiel illustriert das grundlegende Prinzip recht anschaulich: durch die Rekursion erfolgt zunächst eine Aufteilung der Datei bis zu einer Länge 1, dann werden die Daten durch den Mischprozess paarweise zusammen gefügt, wobei gleichzeitig die Sortierung stattfindet. Die genaue Implementation dieses Prozesses ist im folgenden Abschnitt erläutert.

3.3 Zur programmiertechnischen Realisierung

3.3.1 Rekursiv:
Zunächst soll hier die rekursive Variante des 2-Wege-Mergesort besprochen werden. Wie schon erwähnt erfolgen im Gegensatz zu Quicksort am Anfang der Funktion die rekursiven Aufrufe, wodurch die aktuelle Datei in der Mitte in 2 Hälften geteilt wird. Dies geschieht solange, bis alle Dateien nur noch die Länge 1 haben, dann erfolgen keine weiteren Rekursionen mehr. Der nächste Schritt ist das Mischen: 2 benachbarte Dateien der Länge x und y werden zu einer Datei der Länge x+y kombiniert, wobei die entstehende Datei sortiert sein soll. Hier macht sich Mergesort die Eigenschaft zunutze, dass Dateien der Länge 1 bereits trivial sortiert sind und somit unter der Eigenschaft kombiniert werden kann, dass die beiden Teildateien bereits sortiert vorliegen. Dies erfordert nun natürlich, dass Mergesort die Dateien beim Vereinen gleich sortiert, was allerdings einfach zu realisieren ist: für die Grundidee benötigt man nur 2 Ganzzahlen auf Arrayindizes. Den ersten Zeiger i initialisiert man mit der Anfangsposition der linken Datei, der zweite Zeiger j erhält den Anfang der rechten Datei. Da man weiß, dass die beiden Dateien schon sortiert sind, kann man wie folgt vorgehen: man durchlaufe mit den beiden Zeigern die Dateien derart, dass die beiden Schlüssel, auf welche i und j zeigen, miteinander verglichen werden. Der kleinere der beiden Schlüssel wird in einen anfangs leeren Zwischenspeicher eingefügt und der mit diesem Schlüssel verbundene Arrayzeiger um eine Position weiter gesetzt. Dieser Vorgang wird solange wiederholt, bis eine der beiden Teildateien erschöpft ist. In diesem Fall kann der Rest der anderen Teildatei an die bisherige Folge angehangen werden - die beiden Dateien sind nun vereint und ergeben eine einzige sortierte Folge.

Zur Realisierung dieses Algorithmus' würde man noch mehrere Marken benötigen, um die Enden der Teildateien abfragen zu können. Es geht aber auch anders: effizienter ist es, die beiden Zeiger derart auszunutzen, dass der eine die Marke für den anderen ergibt. Somit wäre folgende rekursive Realisierung denkbar:

void mergesort(int a[], int l, int r){		//l=linker Rand, r=rechter Rand
    if(r>l){
        int i, j, k, m;				//Variablen deklarieren
        m=(r+l)/2;				//Mitte ermitteln
        mergesort(a, l, m);			//linke Teildatei
        mergesort(a, m+1, r);			//rechte Teildatei
        for(i=m+1; i>l; i--) b[i-1]=a[i-1];	//linke  Teildatei in Hilfsarray
        for(j=m; j<r; j++) b[r+m-j]=a[j+1];	//rechte Teildatei umgedreht in Hilfsarray
        for(k=l; k<=r; k++)
            a[k]=(b[i]<b[j])?b[i++]:b[j--];	//füge sortiert in a ein
    }
}

Zu beachten ist, dass man ein globales Hilfsfeld b[] zur Verfügung stellen muss, welches die gleiche Dimension wie das zu sortierende Feld a[] hat. Ein Sortieren eines Feldes a[] erfolgt dann durch den Aufruf von mergesort(a,0,n-1); wobei n die Elementeanzahl darstellt.
Zur Analyse: besteht die Datei aus mehr als 1 Element (r>l), so folgen zunächst die rekursiven Aufrufe für linke und rechte Teildatei. Dann werden diese beiden Teildateien aus Array a[] in das Hilfsarray b[] übertragen. Die erste for-Schleife ist für die linke Teildatei zuständig und speichert sie in der Reihenfolge in b[] ab, wie sie auch schon in a[] vorkommt. Dabei ist zu beachten, dass i zu Beginn auf das letzte Element der Teildatei gesetzt ist und bis zum linken Rand dekrementiert wird. Dass dies Sinn macht, wird gleich verdeutlicht. Die zweite for-Schleife kümmert sich um die rechte Teildatei. j wird vom Anfang der Teildatei ausgehend solange inkrementiert, bis es den rechten Rand erreicht hat. Die Abspeicherung dieser Teildatei in b[] erfolgt allerdings in umgekehrter Reihenfolge.
Die Zeiger i und j werden jetzt nur noch für das Auslesen aus dem Hilfsfeld verwendet: i steht auf dem linken Rand der Datei und somit auf dem kleinsten Element der linken Teildatei, j zeigt auf den rechten Rand der Datei und auch auf das kleinste Element der rechten Teildatei, da diese in umgekehrter Reihenfolge in das Hilfsfeld eingefügt wurde. Warum das Ganze? Ganz einfach: man benötigt keine weiteren Marken zur Prüfung des Endes der beiden Teildateien. Man muss nur mit der dritten for-Schleife die Elemente vergleichen, auf welche die beiden Zeiger zeigen. Das kleinere von beiden wird zurück in a[] eingefügt und der Zeiger im Falle von i eine Position weiter, im Falle von j eine Position zurück gesetzt. Ist eine der beiden Folgen erschöpft, so steht dessen Zeiger auf dem größten Element der anderen Folge und verharrt dort, bis deren Feldzeiger zum selben Element gelangt. Dieses letzte Element wird noch in a[] eingefügt und die letzte for-Schleife terminiert, da alle Elemente betrachtet wurden - die beiden Teildateien sind miteinander verschmolzen und die entstandene Datei ist sortiert.

Folgendes selbst gewählte Beispiel verdeutlicht ausführlich die Vorgehensweise des obigen Algorithmus':

1.) Zunächst werden die beiden schon sortierten Teildateien aus a[] nach b[] verschoben, wobei die rechte Teildatei in umgekehrter Reihenfolge in b[] eingeordnet wird.
2.1) Nun erfolgt die Rückverschiebung nach a[]. i steht zu Beginn auf dem linken, j auf dem rechten Rand der Datei und auf den jeweils kleinsten Elementen der beiden Folgen. Das Element, auf das i zeigt, ist kleiner als das Element von j (1<2), also wird 1 nach a[] verschoben und i inkrementiert.
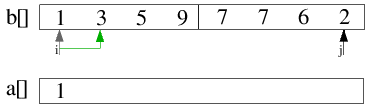2.2) 3 ist größer als 2, also wird 2 in a[] eingefügt und j dekrementiert.
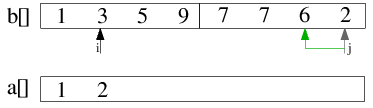2.3) 3<6, also 3 in a[] einfügen und i inkrementieren.
2.4) 5<6, also 5 in a[] einfügen und i inkrementieren.
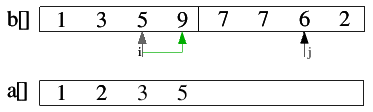2.5) 9>6, also 6 in a[] einfügen und j dekrementieren.
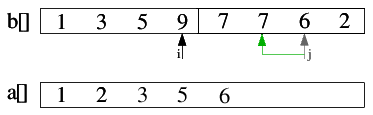2.6) 9>7, also 7 in a[] einfügen und j dekrementieren.
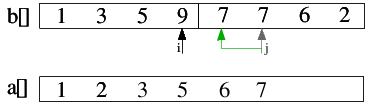2.7) 9>7, also 7 in a[] einfügen und j dekrementieren.
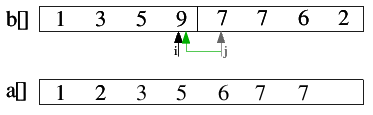2.8) j zeigt auf das letzte Element der linken Teilfolge, auf das auch i zeigt. Dieses letzte Element 9 wird nach a[] verschoben - die beiden sortierten Teildateien wurden zu einer sortierten Datei gemischt und der Algorithmus ist beendet.

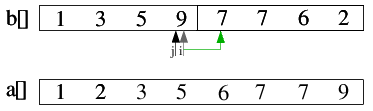3.3.2 Iterativ
Im Gegensatz zu Quicksort lässt sich eine iterative Variante von Mergesort recht gut realisieren, vor allem weil die zu sortierende Datenfolge sequentiell abgearbeitet werden kann und kein zusätzlicher Speicherplatz für einen Hilfsstapel benötigt wird, der die Grenzen von Teilfolgen abspeichern muss.
Das sogenannte Bottom-up-Mergesort ist die einfachste Realisierung eines iterativen Mergesort's. Dabei wird die Liste fortwährend durchlaufen, wobei bei jedem Durchlauf die zu kombinierende Folgenlänge verdoppelt wird. So beträgt diese Länge beim ersten Durchlauf 1, sodass benachbarte Folgen der Länge 2 gebildet werden. Beim zweiten Durchlauf werden dann Folgen der Länge 4, beim dritten der Länge 8 usw. erstellt, bis die Datei aus nur noch einer Folge besteht. Wichtig ist anzumerken, dass die Mischoperationen bei der iterativen Variante nicht denen bei der Rekursion gleichen. Da bei der Rekursion stets in 2 Teile zerlegt wird und bei der iterativen Variante sequentiell benachbarte Dateien gleicher Länge kombiniert werden, handelt es sich z.B. bei einer Folge mit 11 Elementen bei der letzten Sortierung mit der rekursiven Version um ein 5-mit-6-Mischen, während bei der Iteration ein 8-mit-3-Mischen ausgeführt wird (die erste Zahl ist hier immer eine Zweierpotenz).
Folgender Code zeigt eine iterative Implementierung des Mergesort-Algorithmus', ein Aufruf der Funktion für ein zu sortierendes Feld a mit n Elementen erfolgt mit mergesort_it(a,n-1); :

void mergesort_it(int a[], int n){		//n+1=Elementezahl, größer 1
    int step, i, j, k, m, l, r;
    for(step=2; step<n*2; step*=2){		//verdopple sequentiell die Dateilänge
        r=-1;					//Anfangswert für rechte Grenze
        while(r<n){				//solange Folge nicht komplett betrachet
            l=r+1;				//linken Rand auf bisher rechte Grenze+1
            r+=step;				//rechten Rand um step erhöhen
            m=(l+r)/2;				//Mitte finden
            if(r>n){				//wenn über das Ziel hinaus geschossen
                r=n;				//dann auf letztes Element setzen
                if(m>r) m=(l+r)/2;		//wenn Mitte hinter r liegt, neu berechnen
            }
            for(i=m+1; i>l; i--) b[i-1]=a[i-1];	//linke  Teildatei in Hilfsarray
            for(j=m; j<r; j++) b[r+m-j]=a[j+1];	//rechte Teildatei umgedreht in Hilfsarray
            for(k=l; k<=r; k++)
                a[k]=(b[i]<b[j])?b[i++]:b[j--];	//füge sortiert in a ein
        }
    }
}

3.4 Ein Beispiel zu rekursivem Mergesort

Das folgende Beispiel zeigt, wie die Teildateien bei rekursivem Mergesort miteinander verbunden und dabei sortiert werden:

1.) Die Ausgangssituation: die Datei wurde durch Rekursion komplett in Teildateien der Länge 1 zerlegt, nun erfolgt paarweises Mischen.
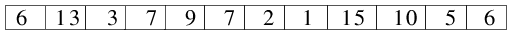2.1) Die ersten beiden Teildateien werden zu einer Datei der Länge 2 gemischt.
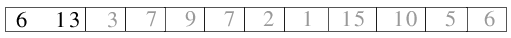2.2) Die zweiten beiden Teildateien werden ebenso zu einer Datei der Länge 2 kombiniert.
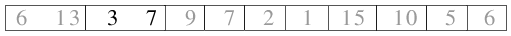2.3) Die beiden entstandenen Dateien der Länge 2 werden zu einer Datei der Länge 4 gemischt.
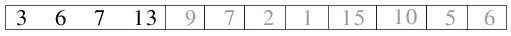2.4) 7 und 9 werden kombiniert...
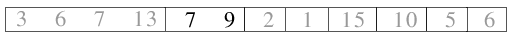2.5) ... ebenso 1 und 2.
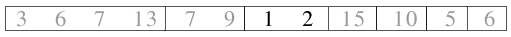2.6) Kombination der beiden Teildateien zu einer Datei der Länge 4.
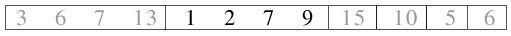2.7) Die beiden bereits sortierten Länge-4-Dateien werden miteinander gemischt.
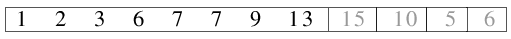2.8) 10 und 15 werden zusammengefügt.
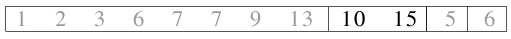2.9.) 5 und 6 kommen zu einer Datei der Länge 2 zusammen.
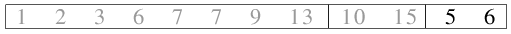2.10) Beide Dateien werden zu einer Länge-4-Datei vereint.
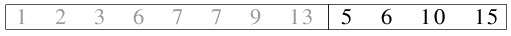3.) Die beiden übrig bleibenden Dateien werden zu einer einzigen sortierten Datei kombiniert - der Algorithmus ist beendet.

3.5 Analyse der Leistungsfähigkeit

Das umstrittene Genie von Neumann hat mit Mergesort schon in der "Computersteinzeit" ein recht einfaches optimales Sortierverfahren entwickelt, welches leicht stabil implementiert werden kann.
Dabei entspricht der günstigste ungefähr dem ungünstigsten Fall, die Anzahl der zu erledigenden Vergleiche variiert kaum. Die Laufzeitkomplexität kann leicht berechnet werden: pro Rekursionsebene werden n Vergleiche ausgeführt, ein Vergleich für jeden betrachteten Schlüssel. Insgesamt gibt es log(n) Rekursionsebenen, da sich pro Schicht die aktuelle Dateilänge halbiert (mit einem Binärbaum vergleichbar). Daraus ergibt sich eine Komplexität von O(n*log(n)), also das Optimum für ein Sortierverfahren.
Der Grund, warum Mergesort Quicksort nicht allgemein bevorzugt wird, ist der, dass es in praxi bei zufälligen Eingabedaten mehr Zeit zum Sortieren beansprucht als Quicksort mit derselben Datei - dies gilt für das grundlegende Quicksort ebenso wie für ein verbessertes Quicksort mit median-of-three und/oder insertion sort zur Behandlung kleiner Teidateien. Der Wertebereich des Geschwindigkeitsvorteils bewegt sich hier von 10-50%. Da bei Mergesort zusätzlicher Speicher benötigt wird, fällt daher eher die Wahl auf Quicksort. Zwischen iterativem und rekursivem Mergesort gibt es ebenfalls noch einmal Geschwindigkeitsunterschiede. Bei o.a. Implementationen ist die rekursive Variante ca. 15% schneller als die iterative Version, auch dies gilt es zu berücksichtigen.
Da Mergesort gegenüber der ursprünglichen Reihenfolge der Eingabedaten unempfindlich ist, ist es bei zufälligen Permutationen genauso effizient wie etwa bei bereits sortierten Folgen. Demgegenüber steht, dass es zu n proportionalen zusätzlichen Speicher benötigt, was bei immer höheren Speicherkapazitäten allerdings kein Problem mehr darstellen dürfte. Zudem ist es als sequentielles und stabiles Verfahren vor allem für Sortierungen von verketteten Listen und auf Externspeicher unentbehrlich, was seine Praxisrelevanz über die Jahre hin gesichert hat.

[ Zurück zum Inhaltsverzeichnis ]