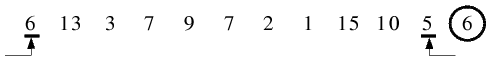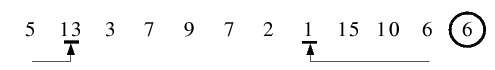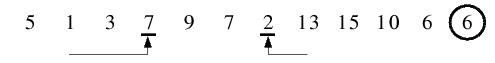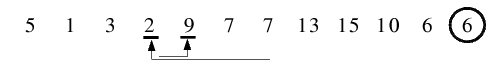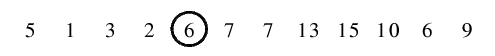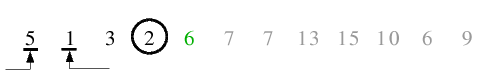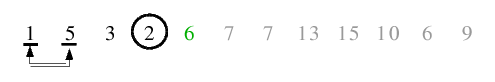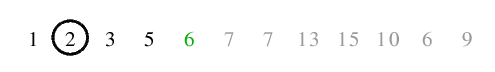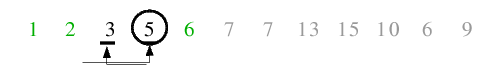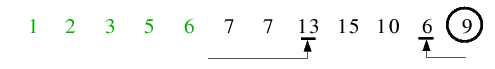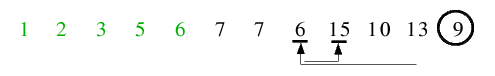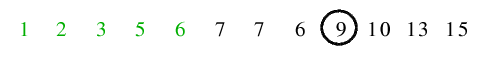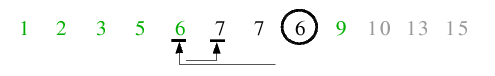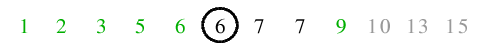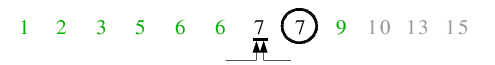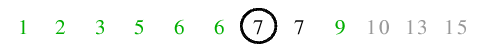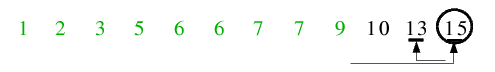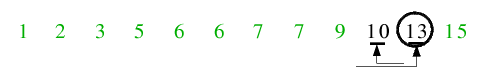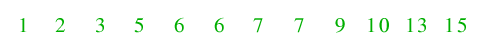2. Quicksort
[ Zurück zum Inhaltsverzeichnis ]
2.1 Historie/Hintergrund
Der grundlegende Quicksort-Algorithmus wurde 1960 von C.A.R. Hoare entwickelt und 1962 veröffentlicht (vgl.
Computer Journal, 5:10-15, 1962) und war seit dem Thema von vielen wissenschaftlichen Untersuchungen.
Quicksort ist der wohl am häufigsten angewandte Sortieralgorithmus, da seine Implementation nicht schwierig ist,
es sich trotzdem sehr gut in vielen Situationen anwenden lässt und oftmals weniger Speicher verbraucht als die
meisten anderen zeitoptimalen Sortierverfahren.
Die Leistungsfähigkeit ist sehr gut erforscht und mathematisch bewiesen, doch auch empirisch bestätigt worden,
womit Quicksort zu einer bevorzugten Methode für ein großes Spektrum von Anwendungen wurde.
Die Vorzüge des Algorithmus': in praxi wird nur durch die Rekursion programmintern ein kleiner Stapel als
Hilfsspeicher benötigt, zudem ist die innere Schleife sehr kurz und im Durchschnitt werden nur
n*log(n) Operationen zum Sortieren von n Schlüsseln benötigt. Dem stehen ein paar, aber mehr theoretische
Aspekte gegenüber: so lässt sich nur schwer eine iterative Variante implementieren, außerdem ist der Algorithmus
störanfällig gegenüber den kleinsten Programmierfehlern. Zudem werden im "worst case" O(n2) Operationen
benötigt, was in der Praxis bei einer guten Implementierung allerdings kaum auftreten dürfte. Weiterhin ist
Quicksort nicht stabil, d.h. die relative Sortiertheit der Datei bleibt nicht erhalten.
Im Laufe der Jahre erschienen immer wieder Verbesserungsvorschläge für Quicksort, meist war es jedoch so, dass
Verbesserungen in einem Teil des Algorithmus' zu Verschlechterungen der Laufzeit in anderen Teilen führten. Am
Ende dieses Artikels soll deshalb nur auf zwei Verbesserungen eingegangen werden, die sich in der Praxis aber
gut bewährt haben: das Finden eines besseren Trennelements mit der Methode median-of-three sowie die Behandlung
kleiner Teildateien mit insertion sort.
2.2 Der Algorithmus
Quicksort ist ein "Teile-und-Herrsche"-Algorithmus ("divide&conquer"). Die Folge der zu sortierenden Daten wird
dabei in 2 Teilfolgen getrennt ("Teile" die Datei), anschließend wird über diese beiden Teildateien unabhängig
voneinander sortiert, indem diese auf dieselbe Art und Weise wie die Ausgangsfolge geteilt werden ("Herrsche"
über die Teilfolgen). Diese Teilungen der Unterfolgen werden solange fortgesetzt, bis nur noch ein Element in
der Teilfolge existiert - dann gilt die Gesamtfolge als sortiert.
Doch wie geschieht dieses "Teilen"? Hierin muss ja das Geheimnis stecken, wie am Ende die gesamte Folge sortiert
sein kann.
Zunächst sucht man sich ein Trennelement (auch Pivotelement), welches idealerweise von der Wertigkeit
her genau in der Mitte der Folge liegt (hierzu gleich noch mehr). Durch das Teilen soll nun Folgendes erreicht werden:
- Alle Elemente links vom Trennelement sollen kleiner oder gleich dem Trennelement sein.
- Alle Elemente rechts vom Trennelement sollen größer oder gleich diesem sein.
- Das Trennelement selbst soll an seine endgültige Stelle in der zu sortierenden Folge gelangen.
Die Auswahl eines geeigneten Trennelements stellt dabei schon eine Wissenschaft für sich dar. Der Einfachheit
halber nimmt man beim grundlegenden Quicksort z.B. das letzte Element der Folge als Trennelement. Wie schon erwähnt
wäre es laufzeitmäßig am besten, wenn das Trennelement von der Wertigkeit her in der Mitte der aktuellen (Teil-) Folge
liegt. Dadurch würde die Folge in zwei gleichgroße Teilfolgen geteilt werden, wodurch sich die Rekursionstiefe des
Algorithmus' gering halten lässt (im Prinzip würde man dadurch einen vollständigen Binärbaum erhalten, doch dazu in
der Analyse mehr). Die Schwierigkeit ist nur, dieses mittlere Element zu finden. In einer unsortierten Folge müsste
man jedes Element zumindest einmal betrachten, was eine Komplexität von O(n) zur Folge hat. Natürlich ist dies
uneffektiv. Eine Alternative ist es, 3 Elemente der Folge auszuwählen und das mittlere Element dieser 3 als Trennelement
auszuwählen. Dies ist noch einfach realisierbar und verbessert die Laufzeit doch spürbar, als wenn man nur ein
beliebiges Element auswählt, da die Wahrscheinlichkeit steigt, dass man ein Element der Folge findet, welches näher
an der Mitte liegt. Dieses Spielchen heißt median-of-three und wird als Verbesserung weiter unten besprochen,
man kann es aber auch weitertreiben: median-of-five, median-of-seven etc. kann man implementieren, wenn man will,
allerdings muss man selber abschätzen, ob sich der dabei betriebene Aufwand in einer besseren Laufzeit widerspiegelt
oder ob man sogar noch Zeiteinbußen hinnehmen muss. Deswegen soll median-of-three genügen und grundlegend das
letzte Element als Trennelement benutzt werden, da es praktisch egal ist, welches Element der unsortieren Folge man
auswählt - die Wahl könnte auch zufällig erfolgen...
Folgendes Bild soll die Absichten der "Teile"-Methode illustrieren:
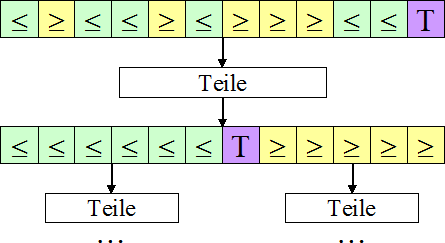
Sehr schön zu sehen ist, dass Elemente, die kleiner oder gleich dem Trennelement sind (grün), durch das Teilen links
von diesem eingeordnet werden, größer-gleich-Elemente (links) hingegen rechts - nun herrscht schon ein viel größeres
Maß an Ordnung als vor dem Teilen. Anschließend erfolgt der rekursive Aufruf von "Teile" getrennt für die entstandene
linke und rechte Teilfolge. Durch das Teilen wird die Folge also derart vorsortiert, dass das Trennelement seine
endgültige Position in der Datei erhält und kein weiteres Mal betrachtet werden muss. Bei den beiden Teildateien kommt
es nachfolgend durch ein weiteres Teilen wiederum zu einer Vorsortierung - dies geschieht rekursiv solange, bis eine
Folge nur noch ein Element enthält - weiter kann nicht sortiert werden, muss auch nicht: denn durch die
Vorsortierungen der größeren Folgen wurde die Folge an sich komplett sortiert.
2.3 Zur programmiertechnischen Realisierung
Das Grundprinzip ist bekannt: man nimmt das letzte Folgenelement als Trennelement und ordnet die Folge so um, dass
alle Glieder, welche kleiner gleich dem Trennelement sind, nach links und größere Elemente nach rechts verschoben
werden. Im Anschluss folgt ein rekursiver Aufruf jeweils getrennt für die linke sowie rechte Teilfolge.
Die Lösung in einer Hochsprache sieht auch entsprechend logisch und einfach aus: man erstellt zwei Ganzzahlen int i
und int j, welche Arrayindizes speichern sollen. Diese initialisiert man mit dem linken Rand der Folge für i und
dem rechten Folgenrand für j. Nun wird mit diesen beiden "Zeigern" die Folge durchlaufen. i wird schrittweise inkrementiert,
durchläuft die Folge also nach rechts. Dies geschieht solange ohne Aktion, bis ein Element gefunden wird, welches größer
oder gleich dem Trennelement ist. An dieser Position bleibt i stehen und es wird damit begonnen, j zu dekrementieren -
solange, bis ein Element gefunden wird, welches kleiner oder gleich dem Trennelement ist. Die Gleichheit wird bei beiden
Tests mit eingeschlossen, da somit eine bessere Ausgeglichenheit der Zerlegung bei vielen identischen Schlüsseln erreicht
werden kann, was mathematisch intensivst untersucht und gezeigt wurde (auch wenn dies ein paar Austauschoperationen mehr zu
erfordern scheint). Wir haben nun ein zum Trennelement relativ "großes" Element im linken Folgenteil und ein "kleines" Element
im rechten Folgenteil gefunden. Um die Vorsortierung zu gewährleisten, werden diese beiden Elemente miteinander vertauscht.
Dann werden die beiden Folgenzeiger weiter in-/dekrementiert und das Tausch-Spielchen solange fortgesetzt, bis beide Zeiger
aufeinander treffen. Ein Problem sollte man aber noch beachten: ist die Folge zu Beginn schon sortiert, so kann i nicht über
den rechten Folgenrand hinauslaufen, da mindestens beim Trennelement gestoppt wird, vorausgesetzt man schließt die Gleichheit
mit ein. Aber: j kann unterlaufen und auf das Element -1 zeigen, wenn die Folge zu Beginn in verkehrt sortierter Reihenfolge
vorliegt. Da kein Element kleiner dem Trennelement gefunden werden kann, läuft j aus dem Feld hinaus, was man natürlich
unterbinden muss. Zu diesem Zwecke muss man noch auf j>i prüfen, wenn man j dekrementiert.
Zurück zum Algorithmus: zum Abschluss wird nun das Trennelement, welches ja immernoch
an letzter Folgenposition steht, mit dem Element getauscht, welches am weitesten links in der rechten Teilfolge steht -
dadurch erhält es seinen endgültigen Platz in der Folge und muss nicht noch einmal betrachtet werden. Anschließend folgen die
rekursiven Aufrufe des Algorithmus' für die linke und rechte Teilfolge ohne dem Trennelement. Diese Rekursion
geschieht solange, bis nur noch ein Element eine Teilfolge darstellt. Da bei jedem Rekursionsaufruf zumindest ein Element von
der bisherigen Folge abgetrennt wird (auf jeden Fall das Trennelement), ist sicher gestellt, dass der Algorithmus terminiert.
Folgende quicksort()-Funktion ist eine mögliche Implementation des grundlegenden Algorithmus' und wird mit quicksort(a,0,n-1) zum
Sortieren des Feldes a mit n Elementen aufgerufen:
void quicksort(int a[], int l, int r){ //a=Array, l=linker Rand, r=rechter Rand
if(r>l){ //solange mehr als 1 Folgenelement existiert
int i=l-1, j=r, tmp; //Variableninitialisierung mit Folgenrändern
for(;;){ //Endlosschleife; bricht ab, wenn i>=j
while(a[++i]<a[r]); //inkrem., bis größeres Element gefunden wird
while(a[--j]>a[r] && j>i); //dekrem., bis kleineres Element gefunden wird
if(i>=j) break; //brich ab, wenn sich die Folgenzeiger treffen
tmp=a[i]; a[i]=a[j]; a[j]=tmp; //tausche kleineres mit größerem Element
}
tmp=a[i]; a[i]=a[r]; a[r]=tmp; //tausche Trennelement
quicksort(a, l, i-1); //rekursiver Aufruf für linke Teilfolge
quicksort(a, i+1, r); //rekursiver Aufruf für rechte Teilfolge
}
}
2.4 Ein Beispiel
Folgendes kommentiertes Beispiel soll den Durchlauf durch das Programm mit o.a. Code illustrieren:
| 1.1) Linker und rechter Folgenzeiger wurden initialisiert, 6 als Trennelement festgelegt. Von links wurde mit 6 ein Element
gefunden, welches größer gleich dem Trennelement ist, von rechts wurde mit 5 ein kleineres Element gefunden. Diese werden
miteinander vertauscht.
|
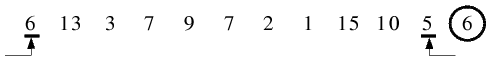 |
| 1.2) Von links wird mit 13 sofort ein Element gefunden, welches größer als das Trennelement 6 ist. Von rechts läuft der
Folgenzeiger bis 1, welches kleiner ist. Diese Element werden wieder getauscht.
|
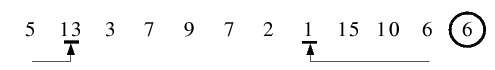 |
| 1.3) 7 wird als größeres, 2 als kleineres Element gefunden und miteinander vertauscht.
|
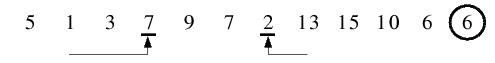 |
| 1.4) Von links wird 9 als größeres, von rechts 2 als kleineres Element gefunden. Allerdings werden diese nicht
miteinander vertauscht, da sich die beiden Folgenzeiger überschneiden und die Endlosschleife terminiert.
|
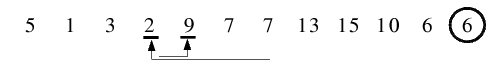 |
| 1.5) Zum Schluss dieser ersten Vorsortierung wird noch das Trennelement mit dem äußerst linken Element der rechten
Teilfolge getauscht und erhält damit seinen endgültigen Platz. Anschließend erfolgen die rekursiven Aufrufe für linke
und rechte Teilfolge. Wie gut zu sehen ist, wurde die Folge in 2 Teile "geteilt": die Elemente in der linken Teilfolge
sind kleiner und die in der rechten Teilfolge größer als das verbindende Trennelement.
|
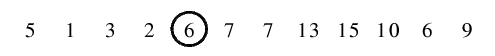 |
| 2.1) Der erste rekursive Aufruf erfolgt für die linke Teildatei. 2 als letztes Element ist Trennelement. Von links
wird 5 als größer und von rechts 1 als kleiner gefunden und miteinander vertauscht.
|
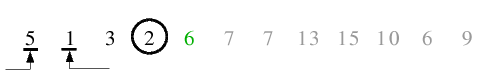 |
| 2.2) Da sich beide Zeiger überschneiden, wird nichts getauscht und die Endlosschleife terminiert.
|
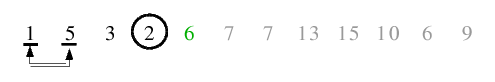 |
| 2.3) Zum Schluss wird das Trennelement wieder an seine endgültige Position an den linken Rand der rechten Teilfolge
getauscht. Der rekursive Aufruf für die linke Teilfolge kehrt sofort zurück, da diese nur aus einem Element besteht, also
folgt der Aufruf für die rechte Teilfolge.
|
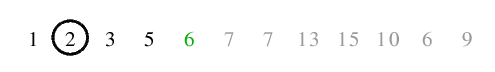 |
| 3.) 5 ist Trennelement. Die beiden Zeiger überschneiden sich sofort nach dem ersten Auffinden von
größer-/kleiner-gleich-Elementen, sodass keine Vertauschungen stattfinden und die Endlosschleife zurückkehrt. Dann erfolgt
das Tauschen des Trennelementes an die linke Position der rechten Teilfolge, welche allerdings schon die momentane Position
des Trennelementes ist - daher kommt es zu keiner Änderung in der Folgenordnung. Die linke Teilfolge enthält 1 Element, die
rechte Teilfolge sogar keines - infolge dessen kehrt die Funktion zurück.
|
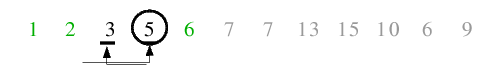 |
| 4.1) Die linke Teildatei der Ausgangsfolge gilt nun als sortiert, da alle Aufrufe bis zur ersten Rekursionsebene zurückkehren.
Nun folgt der Aufruf für die rechte Teildatei. Zunächst ist 9 Trennelement, der linke Zeiger führt zur 13 als größeres und der
rechte Zeiger zu 6 als kleineres Element, welche folglich miteinander vertauscht werden.
|
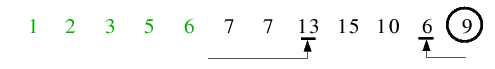 |
| 4.2) Beim nächsten Halt der beiden Zeiger überschneiden sich diese schon, sodass die Endlosschleife abbricht.
|
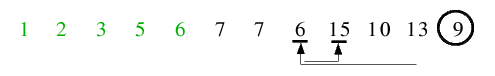 |
| 4.3) Nach dem Tausch des Trennelementes an seine endgültige Position erfolgt der Aufruf für die linke Teilfolge.
|
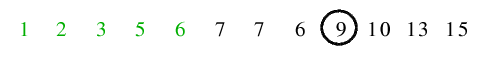 |
| 5.1) 6 ist Trennelement, die Endlosschleife terminiert bereits beim ersten Anhalten der Zeiger, da der rechte Zeiger auf einem
kleineren Index steht als der linke Zeiger.
|
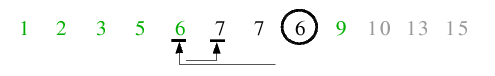 |
| 5.2) Das Trennelement wird auf seine Endposition getauscht. Die linke Teildatei ist leer, daher erfolgt der Aufruf für die
rechte Teilfolge.
|
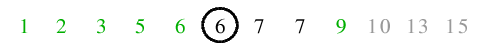 |
| 6.1) 7 ist Pivot, nach dem Lauf der beiden Zeiger stehen diese auf demselben Element, sodass die Endlosschleife abbricht.
|
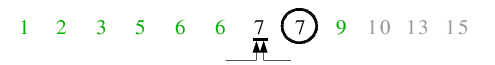 |
| 6.2) Das Trennelement kommt auf seine endgültige Position und die Funktion kehrt zurück.
|
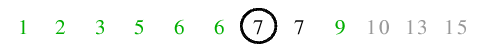 |
| 7.1) In dieser äußerst rechten Teilfolge ist 15 das Pivot. Die beiden Zeiger überschneiden sich wieder sofort nach dem ersten
Durchlauf, sodass nichts getauscht wird, nur das Trennelement noch an seine korrekte Position gelangt, auf welcher es sich jedoch
schon befindet, sodass keine Reihenfolgeänderungen stattfinden.
|
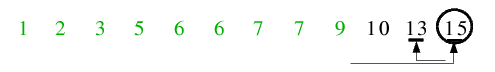 |
| 7.2) Zu guter letzt erfolgt der Aufruf für diese linke Teilfolge. 13 ist Trennelement, der erste Halt der Zeiger führt gleich
zu einem Abbruch der Endlosschleife, sodass nichts getauscht wird und das Trennelement hat schon seine Endposition inne.
|
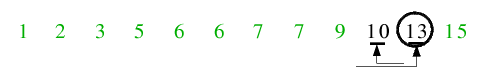 |
| 8.) Alle Aufrufe kehren zurück bis zur ersten Rekursionsebene. Dort wurden linke und rechte Teildatei behandelt, sodass auch
dieser Aufruf beendet ist - die Folge gilt als sortiert!
|
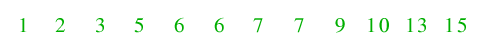 |
2.5 Verbesserungen
2.5.1 Besseres Trennelement finden (Median-of-three)
Als Einleitung zu dieser Quicksort-Verbesserung zunächst noch einmal folgende Betrachtungen:
1.) Günstigster Fall: dieser tritt beim Quicksort-Algorithmus dann ein, wenn das betrachtete Teilfeld bei jedem Aufruf von
quicksort() in zwei gleich große Stücke zerteilt wird.
2.) Ungünstigster Fall: diesen beobachtet man dann, wenn eines der beiden Stücke nur ein
Element enthält. In diesem ungünstigsten Fall ruft sich quicksort() N-mal selber auf (N=Anzahl der Feldelemente), zudem
benötigt der Algorithmus N2/2 Vergleiche, hat also dieselbe Laufzeitkomplexität wie BubbleSort, welches
man ja nicht wirklich als effizient bezeichnen kann.
Der ungünstigste Fall kann demnach z.B. dann eintreten, wenn man a[r] als zerlegendes Element nimmt und den Quicksort auf
ein bereits sortiertes Feld loslässt. Eine sehr einfache Möglichkeit in diesem Fall wäre es, das Element a[(l+r)/2] als
Trennelement zu benutzen, welches ja das (vom Index her) mittlere Feldelement darstellt. Hierbei kann es allerdings genauso
leicht passieren, dass man ein Element erwischt, welches an einem der beiden Enden der Werteskala der Feldelemente
angesiedelt ist, doch die Chance dafür ist schon geringer.
Eine sehr einfache und augenscheinlich sinnvolle Lösung ist hingegen, drei Elemente aus dem Feld zu entnehmen und
das (wertmäßig) mittlere von ihnen als Trennelement zu betrachten. Zufallsgeneratoren sind in diesem Fall übertrieben, eine
einfache Lösung des Herausnehmens der drei Elemente besteht darin, das erste Element mit a[l], das zweite mit a[(l+r)/2]
und das dritte Element mit a[r] fest zu legen. Das Herausfinden und der Austausch zwischen den Elementen findet wie im
folgenden C-Code gezeigt statt:
int m=(l+r)/2;
if(a[l]>a[m])
{ tmp=a[l]; a[l]=a[m]; a[m]=tmp; }
if(a[l]>a[r])
{ tmp=a[l]; a[l]=a[r]; a[r]=tmp; }
else if(a[r]>a[m])
{ tmp=a[r]; a[r]=a[m]; a[m]=tmp; }
Es ist zu erkennen, dass sich das wertmäßig mittlere Element der drei nach der Anwendung dieses Algorithmus' an der Stelle
a[r] befindet. Dies hat Vorteile, da somit dieses Element vom Zähler j des Quicksort-Algorithmus nicht betrachtet werden
muss und es sogleich an seine Stelle im sortierten Feld eingeordnet wird. Das spart natürlich Rechenzeit.
Die alles entscheidende Frage: Was bringt uns das? Die Beantwortung ist nicht leicht und es kann keine allgemeine
Leistungskenngröße geben, was ganz einfach zu erklären ist: auch beim Herausnehmen und Vergleichen von drei Elementen kann
es dazu kommen, dass man eben die drei größten bzw. kleinsten Elemente entnimmt, speziell kann ohne Verwendung eines Zufallsgenerators
natürlich auch ein Feld konstruiert werden, welches sich am ungünstigsten für diesen Fall verhält. In der Praxis, und hier
gehen wir vom Durchschnitt der Fälle aus, wird die Chance, eines der mittleren Elemente zu treffen, jedoch deutlich erhöht
und somit erhöht sich natürlich auch die Wahrscheinlichkeit, dass ein Feld in zwei etwa gleich große Teilfelder zerlegt
wird. Im Allgemeinen kann man von einer Geschwindigkeitssteigerung von 5% und (eher) mehr ausgehen.
Hier noch einmal der komplette verbesserte Quicksort-Algorithmus mit der Methode "median of three":
void qsort_median(int a[], int l, int r){
if(r>l){
int i=l-1, j=r, tmp;
if(r-l > 3){ //Median of three
int m=(l+r)/2;
if(a[l]>a[m])
{ tmp=a[l]; a[l]=a[m]; a[m]=tmp; }
if(a[l]>a[r])
{ tmp=a[l]; a[l]=a[r]; a[r]=tmp; }
else if(a[r]>a[m])
{ tmp=a[r]; a[r]=a[m]; a[m]=tmp; }
}
for(;;){
while(a[++i]<a[r]);
while(a[--j]>a[r] && j>i);
if(i>=j) break;
tmp=a[i]; a[i]=a[j]; a[j]=tmp;
}
tmp=a[i]; a[i]=a[r]; a[r]=tmp;
qsort_median(a, l, i-1);
qsort_median(a, i+1, r);
}
}
2.5.2 Behandlung kleiner Teilfelder
Neben der Überlegung, wie kleine Teilfelder zu vermeiden sind (median-of-three), kann man sich auch über die Behandlung
solcher Gedanken machen. Wenn man sich den klassischen Quicksort anschaut, so stellt man fest, dass die Zerlegung (die
rekursiven Funktionsaufrufe) für viele kleine Teilfelder bis hin zur Feldgröße 1 stattfindet. Folglich kann man festlegen,
dass eine Möglichkeit gefunden werden muss, Quicksort für kleine Teilfelder schneller ablaufen zu lassen. Eine Möglichkeit,
die oft angewandt wird, besteht darin, insertion sort auf ein Teilfeld loszulassen, falls die Größe des Feldes unter
einen konstanten Schwellwert M sinkt. Dieser Quick-/Insertion-Sort-Mix lässt sich in C-Notation wie folgt darstellen:
void qsort_ins(int a[], int l, int r){
int i, j, tmp;
if(r-l > M){ //Quicksort
i=l-1; j=r;
for(;;){
while(a[++i]<a[r]);
while(a[--j]>a[r] && j>i);
if(i>=j) break;
tmp=a[i]; a[i]=a[j]; a[j]=tmp;
}
tmp=a[i]; a[i]=a[r]; a[r]=tmp;
qsort_ins(a, l, i-1);
qsort_ins(a, i+1, r);
}
else{ //insertion sort
for(i=l+1; i<=r; ++i){
tmp=a[i];
for(j=i-1; j>=l && tmp<a[j]; --j)
a[j+1]=a[j];
a[j+1]=tmp;
}
}
}
Ist die Bedingung if(r-l > M) nicht mehr erfüllt (ist das Teilfeld also "zu klein" für Quicksort), so wird für das
behandelte Teilfeld insertion sort aufgerufen, ansonsten findet weiterhin das klassische Quicksort Anwendung.
Was bringt's?: Mit dieser Methode lassen sich viele rekursive Aufrufe sparen. In Abhängigkeit von M kann man
Laufzeitverbesserungen von 20% und mehr beobachten, was wahrlich nicht zu unterschätzen ist.
Eine zweite Vorgehensweise in dieser Hinsicht beruht auf der Tatsache, dass insertion sort für sortierte Felder linear abläuft
und für fast sortierte Felder effizient arbeitet. Also kann man o.a. Algorithmus so variieren, dass zunächst Quicksort aufgerufen
wird, aber nicht mit der Abfrage if(r>l), sondern mit dem Vergleich if(r-l > M). Somit werden kleine Teilfelder von
Quicksort gänzlich ignoriert. Zu seinem sortierten Feld kommt man schlussendlich, indem man dieses vorsortierte Feld einmal
komplett von insertion sort durchlaufen lässt, welches in diesem Fall effektiv arbeitet. Trotzdem ist diese Vorgehensweise
etwas uneffektiver als die zuerst vorgestellte, weshalb man obigen Code der folgenden C-Notation doch vorziehen sollte:
//Hilfsfunktion für qsort_ins2()
void qsort_M(int a[], int l, int r){
int i, j, tmp;
if(r-l > M){ //Quicksort
i=l-1; j=r;
for(;;){
while(a[++i]<a[r]);
while(a[--j]>a[r] && j>i);
if(i>=j) break;
tmp=a[i]; a[i]=a[j]; a[j]=tmp;
}
tmp=a[i]; a[i]=a[r]; a[r]=tmp;
qsort_M(a, l, i-1);
qsort_M(a, i+1, r);
}
}
//2. Variante von Quick-/insertion-sort
void qsort_ins2(int a[], int l, int r){
int i, j, tmp;
qsort_M(a, l, r); //qsort_M zur Vorsortierung
for(i=l+1; i<=r; ++i){ //insertion sort
tmp=a[i];
for(j=i-1; j>=l && tmp<a[j]; --j)
a[j+1]=a[j];
a[j+1]=tmp;
}
}
2.5.3 Optimale Wahl von M
Bleibt noch die Frage offen, wie groß man den Schwellwert M festlegen sollte. Folgendes Diagramm zeigt die Laufzeit bei N=10 bis
N=60 Mio. Elementen in Abhängigkeit von M=0 bis M=100:
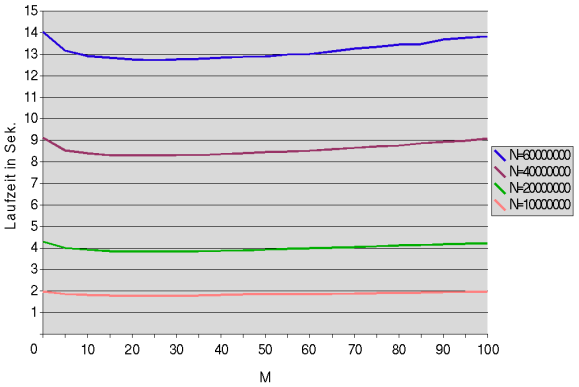
Man sieht, dass M unabhängig von N zu sein scheint und ca. bei M=25 die besten Ergebnisse liefert. Diesen Wert sollte
man auch für M wählen, um die Verbesserung mit Insertion Sort optimal wirken zu lassen.
2.5.4 Beides zusammen?
Natürlich könnte man nun auf die Idee kommen, die beiden Verfahren zu kombinieren und somit eine noch größere Effizienzsteigerung
zu erreichen. Dieses Vorgehen ist im folgenden C-Code fest gehalten:
void qsort_comb(int a[], int l, int r){
int i, j, tmp;
if(r-l > M){ //Quicksort
i=l-1; j=r;
if(r-l > 3){ //Median of three
int m=(l+r)/2;
if(a[l]>a[m])
{ tmp=a[l]; a[l]=a[m]; a[m]=tmp; }
if(a[l]>a[r])
{ tmp=a[l]; a[l]=a[r]; a[r]=tmp; }
else if(a[r]>a[m])
{ tmp=a[r]; a[r]=a[m]; a[m]=tmp; }
}
for(;;){
while(a[++i]<a[r]);
while(a[--j]>a[r] && j>i);
if(i>=j) break;
tmp=a[i]; a[i]=a[j]; a[j]=tmp;
}
tmp=a[i]; a[i]=a[r]; a[r]=tmp;
qsort_comb(a, l, i-1);
qsort_comb(a, i+1, r);
}
else{ //insertion sort
for(i=l+1; i<=r; ++i){
tmp=a[i];
for(j=i-1; j>=l && tmp<a[j]; --j)
a[j+1]=a[j];
a[j+1]=tmp;
}
}
}
Doch Vorsicht: dieser Algorithmus kann uneffektiver sein als der zuvor vorgestellte insertion-/Quicksort-Mix! Grund: wählt man
einen großen Schwellwert M, für welchen Quicksort in insertion sort übergeht, so ist die Chance gering, in einer Teildatei, welche ja
mindestens die Größe M haben muss, als Trennelement eines heraus zu greifen, welches sich im oberen bzw. unteren Teil des Feldes befindet.
Somit kann es unangebracht sein, ein median-of-three (also das wertmäßig mittlere von drei Elementen) zu ermitteln, da die Vergleiche
und Austauschoperationen hierbei mehr Rechenzeit kosten können als wie sie ersparen. Es ist also eher eine Gewissensfrage, ob man
median-of-three und das insertion-sort-Verfahren für kleine Teilfelder kombiniert. Im Allgemeinen wird dadurch Rechenzeit erspart,
trotzdem kann selbst bei zufälligen Permutationen allein die Verbesserung mittels insertion sort schneller sein.
Zu kombinieren empfehle ich beide Verfahren bei optimal gewähltem M, wobei auch bei der Mischung mit median-of-three M=25 am effektivsten
ist, doch auch dies ist subjektiv zu entscheiden und kann nicht verallgemeinert werden.
2.6 Laufzeitbetrachtungen
Ein Durchlauf von Quicksort lässt sich gut als Binärbaum darstellen. Folgende Abbildung zeigt obiges Beispiel: dabei
ist ein Knoten des Baumes jeweils das aktuell gewählte Trennelement, ein linker Sohn ist das Trennelement der linken, ein rechter Sohn
das Trennelement der rechten Teilfolge. Anhand dieses Binärbaumes lassen sich gute Aussagen über die Laufzeit des Algorithmus' treffen,
so entspricht die Höhe des Baumes z.B. der Rekursionstiefe für eine Sortierung der gegebenen Folge.
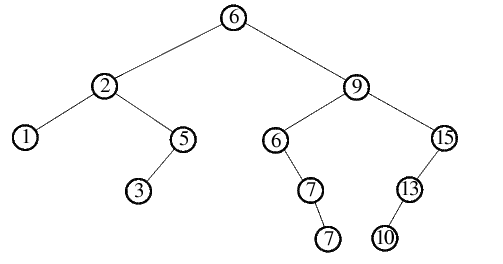
Wie schon erwähnt, tritt der günstigste Fall dann ein, wenn bei allen rekursiven Aufrufen die jeweilige Folge in 2 gleichgroße Teilfolgen
zerlegt wird. Dies geschieht, wenn stets das wertmäßig mittelste Element der Teilfolge als Pivotelement gewählt wird (dass dies nicht so
einfach geht, wurde ja schon ausführlich besprochen). Schauen wir uns den Binärbaum für obiges Beispiel an, wenn immer
das beste Pivotelement anstelle des letzten Elements gewählt worden wäre:
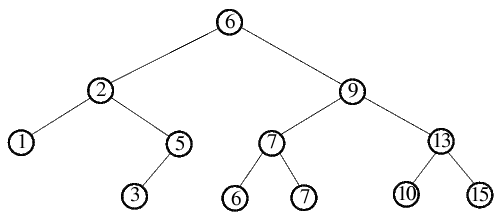
Hätte die Folge noch 3 Elemente mehr gehabt, so würde es sich hierbei um einen vollständigen Binärbaum handeln, d.h. jeder Knoten
des Baumes hätte stets 2 Söhne. Doch auch so kann man die Ausgeglichenheit erkennen - die Höhe des Baumes und damit auch die Rekursionstiefe
ist für diese Anzahl von Elementen minimal. Was bedeutet das? Pro Rekursionsschicht werden bei einem vollständigen Binärbaum rund n
Schlüsselvergleiche durchgeführt, da jedes Element bis auf die vorigen Pivotelemente einmal betrachet und mit dem jeweiligen Pivot verglichen
wird. Ein vollständiger Binärbaum hat die Höhe log(n), sodass man im günstigsten Fall also auf n*log(n) Schlüsselvergleiche kommt.
Im Gegensatz dazu tritt der ungünstigste Fall ein, wenn bei einem Rekursionsaufruf immer nur genau ein Element abgespalten wird. Der zugehörige
Binärbaum würde zu einer verketteten Liste entarten, wie es folgende Abbildung für das gegebene Beispiel zeigt:
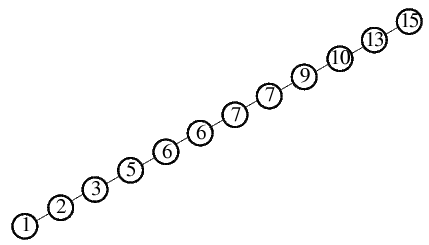
Dazu müsste immer das momentan größte (bzw. immer das momentan kleinste) Element der Folge als Trennelement ausgewählt werden. Wenn wir das
grundlegende Quicksort nehmen würden, wo immer das letzte Element als Pivot gewählt wird, wäre der ungünstigste Fall dann gegeben, wenn die
Folge bereits auf- bzw. absteigend sortiert vorliegt. Durch median-of-three könnte man dies schon einmal vermeiden.
Für die Abspaltung eines Elementes benötigt man pro Rekursionsschicht ca. n/2 Vergleiche, die Höhe des Baumes und die damit
verbundene Rekursionstiefe beträgt n. Somit ergibt sich für den ungünstigsten Fall eine Anzahl von n2/2
Schlüsselvergleichen.
Und was lässt sich über den mittleren Fall aussagen? Es zeigt sich, dass bei zufälligen Permutationen der grundlegende Quicksort-Algorithmus
im Mittel nicht viel schlechter arbeitet als im günstigsten Fall, die Wahl des Pivots also im Schnitt auf ein mittleres Element fällt.
So lässt sich zeigen, dass die Zahl der Schlüsselvergleiche nur um 38% höher ist als im best case - daher lässt sich sagen:
Im Mittel benötigt Quicksort ungefähr 2*n*ln(n) Schlüsselvergleiche.
Und dieser gute durchschnittliche Fall ist auch einer der Hauptgründe, warum sich Quicksort über die Jahre hinweg als eines der beliebtesten
Sortierverfahren etabliert hat.
[ Zurück zum Inhaltsverzeichnis ]