Einführung in Künstliche Neuronale Netze

Ein informatisch sehr anspruchsvolles, zukunftsorientiertes und nicht zuletzt auch algorithmisch interessantes Thema sind künstliche neuronale Netze. Eine kleine Einführung in die Thematik zur besseren Vorstellung des Sinns und Aufbaus solcher Netze soll nachfolgend gegeben werden...

Einleitung

Das Gehirn des Menschen ist wohl eines der bemerkenswertesten Errungenschaften der Evolution. Schon seit vielen Jahren versuchen Wissenschaftler in die Tiefen der komplizierten Verschaltungen, gebildet durch Milliarden und Abermilliarden von Nervenzellen, vorzudringen und die Prozesse zu verstehen, die es dem Menschen erlauben, zu denken und zu lernen. Im Zeitalter der Informationstechnik bleiben solche Forschungen natürlich nicht lange unangetastet von Ingenieuren und Informatikern. Wie schon sooft ist die Natur auch hier Vorbild des Menschen, der versucht, das neuronale Netz des Gehirns für informationstechnische Zwecke zu benutzen.
Die Ziele von künstlichen neuronalen Netzen können dabei sehr unterschiedlich sein: Verwendung finden sie bei der Aufdeckung von Kreditkartenbetrug, bei der optischen Zeichen- und Mustererkennung, bei der Überwachung des Zustandes von technischen Maschinen, bei Autopiloten für Straßenfahrzeuge und vielem mehr. Und dies war nur ein kleiner Auszug - vor allem aber geht die Entwicklung in dieser Richtung schnell voran und immer neue Anwendungsgebiete werden erschlossen. Ein interessantes Teilgebiet ist hier auch eine neue Form der KI durch Kopplung alt-bewährter KI-Methoden mit neuronalen Netzen. In Zukunft wird hier sicher mit vielen Entdeckungen zu rechnen sein...

Biologische Zusammenhänge

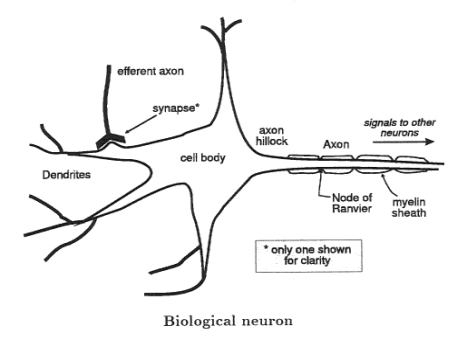
Ein natürliches neuronales Netz, wie es unser Gehirn darstellt, besteht aus Milliarden kleinster Neuronen. Biologische Neuronen sind Nervenzellen, welche Signale empfangen und weiterleiten können. Sie haben einen Zellkörper, von dem mehrere Dendriten ausgehen. Dies sind quasi die "Eingangsleitungen" des Neurons - an den Dendriten empfängt die Nervenzelle Signale von anderen Nervenzellen. Außerdem geht vom Zellkörper aus genau ein Axon ab. Über das Axon sendet ein Neuron Signale - ein Axon stellt somit die "Ausgangsleitung" eines Neurons dar. Das Axon mündet in mehrere Synapsen (Verzweigungen der Ausgangsleitung), so dass die Nervenzelle mit mehreren anderen Nervenzellen "kommunizieren" kann. Allerdings geht die Kommunikation immer nur in eine Richtung: Synapse -> Dendrit -> Zellkörper -> Axon -> Synapse...
Folgende Bilder sollen das Aussehen eines biologischen Neurons und seinen Aufbau illustrieren...

Das Signal, das von Neuron zu Neuron weitergeleitet wird, ist ein elektrischer Impuls. Die Übertragung von den Synapsen des einen auf die Dendriten eines anderen Neurons findet auf chemischem Wege statt. Erhält eine Nervenzelle an ihren Dendriten ein Signal, wird dies nicht direkt weitergeleitet, sondern erst "verarbeitet" - wie in einer Art "Mini-Prozessor". Die einzelnen empfangenen Signale werden in der Regel aufsummiert - wird dabei ein gewisser Schwellenwert erreicht bzw. überschritten, dann wird das Signal über das Axon zum nächsten Neuron weitergeleitet. Für die Weiterleitung gilt die "Alles-oder-Nichts"-Regel, d.h. ein Signal wird entweder gesendet oder nicht (abhängig vom Schwellenwert) - wenn es aber gesendet wird, dann in voller Stärke. Das weitergeleitete Signal kann dann im Folgenden entweder eine induzierende oder hemmende Wirkung haben (Verstärkung/Auslöschung).

Künstliche Neuronale Netze (KNNs)

Bei künstlichen Neuronalen Netzen haben sich die Informatiker viel von den natürlichen Vorbildern abgeschaut: KNNs lernen durch Verstärkung/Dämpfung und Herstellen/Lösen von Verbindungen. Auch ein KNN besteht aus einer Menge von Neuronen, die miteinander auf eine fest vorgegebene oder sich anpassende Struktur verbunden sind und jedes für sich ankommende Signale als eine Art Mini-Prozessor verarbeiten.
KNNs können mittels Software ebenso wie mit Hardware realisiert werden - letzteres ist besonders interessant in Beziehung mit der Erkennung von Störungen technischer Anlagen: Sensoren liefern dabei die Eingabedaten, spezielle Schaltwerke stellen die Neuronen dar, welche durch elektrische Leitungen miteinander verbunden sind und die empfangene Daten verarbeiten können.
Für mich interessanter und hier näher zu betrachten ist allerdings die softwaretechnische Sicht, für die es sehr viele Anwendungen und algorithmische Lösungen gibt.
Im Allgemeinen soll ein KNN nicht das biologische Gehirn nachbilden, dieses dient nur als Vorbild für ein neues System an Probleme heranzugehen, welche zu ihrer Lösung eine Anpassung von bestimmten Faktoren erfordern. Ein KNN, wie der Begriffsteil "Netz" schon impliziert, wird realisiert als Graph ("Netz") mit Knoten, die über Kanten in wohldefinierter Weise miteinander verbunden sind. Der allgemeine Aufbau soll durch folgende Abbildung dargestellt werden:

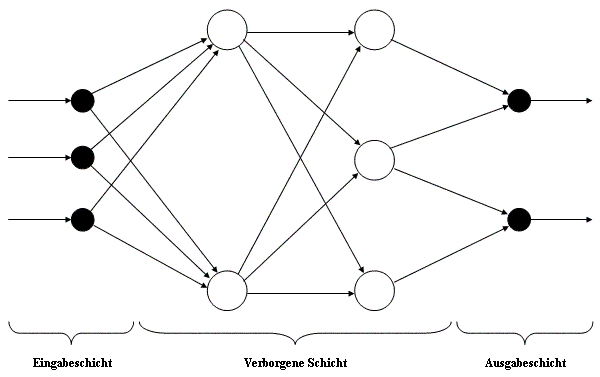
Dies stellt ein einfaches Feedforward-Netz dar, was heißt, dass die Verbindungen zwischen den einzelnen Neuronen nur in Richtung Eingabeschicht->Ausgabeschicht erfolgen und Verbindungen zwischen allen Neuronen der Schicht n mit jedem Neuron der Schicht n+1 existieren. Neuronen der Eingabeschicht sind nur zum Verteilen der Eingabedaten an die nächsthöhere Schicht gedacht, ihre Anzahl entspricht der Anzahl der Eingabedaten. In der verborgenen Schicht findet die eigentliche Verarbeitung statt. Hier können auch mehrere Schichten vorhanden sein, wobei diese Schichten keinen Kontakt zur Umgebung mittels Eingabe-/Ausgabeleitungen haben, von außen also nicht sichtbar sind. Anders die Neuronen der Ausgabeschicht. Ihre Anzahl entspricht der Anzahl der ausgegebenen Werte. Sie verarbeiten ebenfalls die Daten der letzten verborgenen Schicht und geben die ermittelten Werte aus.
Erweitern wir die Sicht des neuronalen Netzes als Verbund von Knoten und Kanten, so beschreiben die folgenden Punkte ziemlich prägnant und vollständig, worum es sich bei einem KNN handelt:

Ein KNN ist eine Menge von einfachen Informationsverarbeitungseinheiten (Knoten des Netzes), die sich über Gewichte (Kanten des Netzes) gegenseitig Signale zusenden. Das Netz ist also gewichtet (enthält Daten an den jeweiligen Kanten) und kann durch sukzessive Veränderung der Gewichte die Lösung eines Problems geben. Ein Gewicht von Neuron i zu Neuron j wird als w_ij bezeichnet.
Von außen betrachtet ist ein KNN eine Einheit, welche Eingabedaten x_i entgegen nimmt und Ausgaben y_i liefert.
WIE die Einheiten miteinander verbunden sind und wieviele Neuronen es pro Schicht gibt hängt vom entsprechenden Netzmodell ab und muss vom Programmierer problemabhängig gewählt werden - Konnektivitätsmuster (Verbundenheitsmuster).
Ein Neuron (Netzeinheit) verfügt zum einen über eine Regel zur Aufnahme der Werte aus den Eingangsverbindungen x_i. Dies gestaltet sich meist als Aufsummierung der Gewichte mal der Werte an den Knoten, von denen die Gewichte ausgehen. Zum Teil muss noch eine Verschiebung erfolgen, welche vom Programmierer geeignet gewählt wird.
Zum anderen wird über eine zweite Regel das empfangene und aufsummierte Signal verarbeitet und an verbundene Neuronen ausgegeben. Diese Regel wird auch als Aktivierungsfunktion bezeichnet, wobei es viele geeignete Funktionen gibt: Beispiele hierfür wären die Identitätsfunktion (y=x), welche die aufsummierten Werte direkt wieder ausgibt, die sigmoide Funktion, logistische Funktionen, vor allem aber auch Schwellenwertfunktionen, die abhängig vom aufsummierten Eingangswert diskrete Ausgangswerte liefern. Prominentes Beispiel wäre hier die binäre Schwellenwertfunktion: ist das Eingangssignal kleiner einem definierten Wert (z.B. <0), so wird 0 ausgegeben, im anderen Fall 1; d.h. je nach Eingangswert findet eine binäre Reaktion des Neurons in Form einer Ausgabe von 0 oder 1 statt. Genaue Beschreibungen der Funktionen würden hier im Rahmen einer Einleitung etwas deplatziert sein - um KNNs verstehen und programmieren zu können, müssen interessierte Leser sowieso zu spezieller Literatur greifen - helfen sollen hier auch die Literaturempfehlungen im Anhang.
Ein neuronales Netz wird nicht im "konventionellen" Sinne programmiert. "Konventionell" soll heißen, dass ein Problem sofort durch einen wohl definierten Algorithmus gelöst wird, der in einem Programm umgesetzt ist. Vielmehr besitzt das KNN zu Programmstart meist zufällige Gewichtswerte, die in einem bestimmten Zahlenintervall liegen. Zum Lösen des Problems, für das das KNN programmiert wurde, durchläuft das Netz eine Art "Lernphase" - hierbei werden dem KNN vom Programmierer/Anwender bestimmte Eingabewerte mit den korrekten Ausgabewerten in einer großen Menge vorgelegt und nach einem geeigneten "Lernalgorithmus" werden die Gewichte im Netz angepasst, bis das Netz zu allen vorgelegten Eingabewerten den korrekten Ausgabewert liefert, wobei eine gewisse Toleranz erlaubt ist (ein sehr bekannter Algorithmus ist dabei die "Backpropagation", welche hier aber nicht näher betrachtet werden soll). Durch die Gewichtsanpassung minimiert das Netz im Prinzip den Fehler, der zu einer falschen Ausgabe geführt hat, bis der Fehler so gering ist, dass die Ausgabe als korrekt erkannt wird. Nach x Durchläufen, wenn zu allen Eingabewerten ein korrekter Ausgabewert geliefert wird, ist die Lernphase beendet. Infolgedessen kann ein Netz in die Test- und Einsatzphase übergeben werden - nun sollte zu jedem problemspezifischen Eingabevektor ein korrekter Ausgabevektor erzeugt werden - wenn der Programmierer alles richtig gemacht hat :)
Die Daten, welche dem Netz in der Lernphase vorgelegt werden, sollten sich prinzipiell von den Daten unterscheiden, welche in der Testphase Verwendung finden - nur so kann gewährleistet werden, dass das Netz eine Lösung des Problems auch für sich ändernde Eingabedaten findet.

Das Wählen der Parameter des Netzes, also die Anzahl der Gewichte, verborgenen Schichten, Neuronen sowie der Regeln für Aufsummieren und die Ausgabefunktion ebenso wie die Wahl eines geeigneten Lernalgorithmus' und die Wahl der Daten, welche in der Lernphase vorkommen und wie oft diese präsentiert werden ist dabei keineswegs trivial und kann als "Wissenschaft für sich" am besten umschrieben werden. Vor allem gibt es keine fest gelegten Regeln, keinen bestimmten Algorithmus, nach dem ein Programmierer vorgehen muss. Liefert ein KNN zu einem gegebenen Problem in der Testphase nicht die richtigen Ergebnisse, so muss das keineswegs heißen, dass sich das Problem durch ein neuronales Netz nicht geeignet modellieren lässt. Viel wahrscheinlicher ist, dass der Programmierer einen Faktor übersehen oder Parameter falsch gewählt hat. Daher ist der Aufbau eines funktionierenden neuronalen Netzes sehr mit "try and error" verbunden - oftmals hilft nichts anderes als ausprobieren, um zu einer funktionierenden Lösung zu gelangen und das macht das Ganze so arg kompliziert. Jedoch sollte es nicht in einer "Rate-Orgie" ausarten und um dies zu vermeiden, muss man zum Einen über fundiertes Wissen im Bereich der neuronalen Netze und zum anderen über sehr viel Wissen auf dem Problem-Gebiet verfügen - schließlich muss darauf das KNN angepasst werden!

Buchempfehlungen

Hier noch ein paar Bücher, welche auch von anderen Autoren für die Problematik empfohlen werden. Wichtig zu wissen ist, dass das Gebiet der neuronalen Netze sehr mathematiklastig ist, was in meinem kurzen Einblick hier sicher kaum zur Geltung kam. Wer also tiefer in die Problematik einsteigen will, sollte z.B. keine Angst vor partiellen Ableitungen von Funktionen mehrerer Veränderlicher haben und die Mathematik nicht scheuen - alle der folgenden Bücher werden hier nämlich mehr oder weniger ins Detail gehen...

Braun, H. Neuronale Netze. Optimiertung durch Lernen und Evolution. Berlin: Springer, 1997
Braun, H., Feulner, J. und Malaka, R. Praktikum Neuronale Netze. Springer, 1996
Callan, R. Neuronale Netze im Klartext. Pearson Studium, 2003
Brause, R. Neuronale Netze. Stuttgart: Teubner, 1995
Dorffner, G. Konnektionismus. Stuttgart: Teubner, 1991
Nauck, D., Klawonn, F. und Kruse, R. Neuronale Netze und Fuzzy-Systeme. Wiesbaden: Vieweg, 1994
Ritter, H., Martinetz, Th. und Schulten, K. Neuronale Netze. Bonn: Addison-Wesley, 1994
Rojas, R. Theorie der Neuronalen Netze. Heidelberg: Springer, 1993
Zell, A. Simulation Neuronaler Netze. Bonn: Addison-Wesley, 1994

Schlussbemerkungen

Bei dieser kleinen Einführung in die Welt der Neuronalen Netze will ich es nun erst einmal belassen. Ich hoffe, dass ich ein wenig das Interesse an dieser wirklich faszinierenden und komplexen Materie wecken konnte. Für weitere Informationen zu künstlichen neuronalen Netzen empfehle ich neben oben benannten Büchern für schneller Interessierte die folgenden Dateien: [ Download 1 ], [ Download 2 ].
Zudem habe ich eine kleine C++-Klasse entworfen, welche ein 3-schichtiges vorwärtsgerichtetes Backpropagationsnetz implementiert. Die nötigen Dateien sind hier zu finden, eine grafische Umsetzung gibt es hier.
Sicher finde ich in Zukunft noch Zeit, mich diesem doch sehr interessanten Thema eingehender zu widmen und auch hierzu den ein oder anderen Artikel zu verfassen...