Beschleunigtes Lernen Neuronaler Netze mit Backpropagation -
Eine empirische Betrachtung am Beispiel von wxANN
Einführung
Dieser Text soll weder eine wissenschaftliche Abhandlung noch eine mathematische Untersuchung des Problems sein, wie man Lernfaktor und Impulsterm zu wählen hat, damit ein Neuronales Netz mit dem Backpropagation-Algorithmus schneller lernt. Wie der Titel schon beschreibt, handelt es sich hierbei vielmehr um eine empirische Betrachtung, unterlegt mit Diagrammen, die anhand vieler Messwerte erstellt wurden und die Probleme verdeutlichen sollen, die mit der Wahl dieser Faktoren einher gehen.Backpropagation
Dieser Mitte der 80er Jahre eingeführte Algorithmus ist das wohl am meisten benutzte Lernverfahren für mehrschichtige vorwärtsgerichtete Neuronale Netze. Eine mathematische Abhandlung würde hier den Rahmen des Artikels sprengen, trotzdem seien an dieser Stelle einige wichtige Formeln gegeben, die zum Verständnis beitragen dürften.Wird ein Neuronales Netz erstellt, so werden die Gewichtsmatrizen zwischen den einzelnen Schichten meist mit kleinen zufälligen Werten belegt. Würde man dem Netz in diesem Status einen Eingabewert präsentieren, so wäre es höchst unwahrscheinlich, dass es zu einer korrekten Ausgabe führen würde. Die Abweichung der Ausgabe des Netzes zu der Ausgabe, die das Netz eigentlich liefern sollte, kann als Summe der quadratischen Fehler berechnet werden:
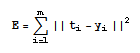
Dabei ist y der IST-Ausgabevektor des Neuronalen Netzes, t hingegen der SOLL-Vektor. Manchmal wird in diesem Zusammenhang auch von der "Energiefunktion" des Netzes gesprochen. Ziel eines Lernverfahrens sollte es nun sein, während der Trainingsphase die Gewichte derart anzupassen, dass sich E, also der Fehler des Netzes, für jeden zu lernenden Eingabevektor minimiert.
Mit anderen Worten muss ein Minimum der Funktion E gefunden werden, welches in den meisten Fällen E=0 ist, da hier das Netz zu jeder Eingabe eine exakte Ausgabe liefert.
Der Backpropagation-Algorithmus funktioniert nun so, dass das Netz zunächst vorwärts durchlaufen wird, um die entsprechenden Ausgabevektoren für jede Schicht zu berechnen. Ist dies geschehen, so wird für die Ausgabeschicht für jedes Neuron der Fehler berechnet (IST-SOLL) und anschließend das Netz rückwärts durchlaufen, um die Gewichte anzupassen.
Aufgrund der Minimum-Bildung liegt es nahe, den Gradienten g der Funktion E zu bestimmen und dann die Gewichte in Richtung des absteigenden Gradienten (also in Richtung -g) zu verschieben, bis ein Minimum erreicht wird bzw. der Fehler ausreichend klein geworden ist. Für ein einzelnes Gewicht würde sich das Verhalten der Fehlerfunktion wie folgt veranschaulichen lassen:
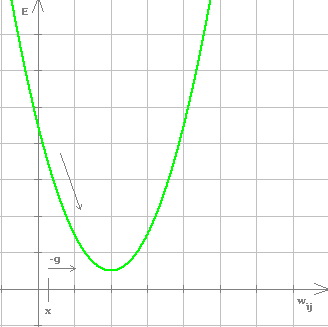
Hier wäre es sinnvoll das Gewicht größer zu wählen, da der absteigende Gradient -g nach rechts zum Minimum zeigt. Backpropagation wird wegen dem Tendieren zum absteigenden Gradienten auch als Gradientenabstiegsverfahren bezeichnet.
Zum Großteil wird als Aktivierungsfunktion für die Neuronen heutzutage die sigmoide Funktion verwendet:
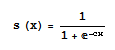
Zur Berechnung des Gradienten benötigen wir die 1. Ableitung dieser Aktivierungsfunktion für jedes Neuron. Die Ableitung der sigmoiden Funktion kann dabei vereinfacht werden zu:
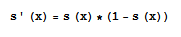
Aus diesem Wissen und dem Kennen des Fehlervektors an der Ausgabeschicht lässt sich nun eine Änderung für die Gewichtsmatrix zwischen der verborgenen und der Ausgabeschicht wie folgt definieren:

Analog dazu kann für andere Schichten die Kettenregel der Differentialrechnung angewendet werden, womit sich für die Gewichtsänderung zwischen Eingabe- und verborgener Schicht ergibt:

Wird dieser Algorithmus in mehreren Iterationsschritten für jeden zu lernenden Eingabevektor ausgeführt, so geht E bei geeigneter Dimensionierung des Netzes und passender Parameterwahl in ein lokales Minimum über. Vorstellen kann man sich das so, dass E "entlang gewandert" wird, bis der Wert der Funktion minimal wird.
Ein großes Problem bei Backpropagation ist der Zeitfaktor: die Konvergenz gegen das Minimum von E ist recht langwierig und rechenintensiv - aus diesem Grund gab es schon viele Ansätze, den Algorithmus zu verbesseren, sodass der Lernprozess schneller erfolgt, sich schneller ein ausreichendes Minimum einstellt. Zwei dieser Verbesserungen sollen hier am Beispiel des von mir erstellten Programms wxANN betrachtet werden, nämlich der Lernfaktor sowie der Impulsterm, welche auch oben schon in den Funktionen zu den Gewichtsänderungen eingeführt wurden.
wxANN besteht zum Großteil aus einem Netz, welches die 10 digitalen Ziffern lernen soll (0-9), um aus einer Matrix mit Pixeln diese Ziffern korrekt zu erkennen.
Der Lernfaktor
Betrachtet man sich die Formeln für die Gewichtsänderungen, dann erkennt man schnell, welchen Einfluss der Lernfaktor hat: als Faktor vor der eigentlichen Gewichtsänderung beeinflusst er direkt und diskret den Wert, mit welchem die Gewichtsänderung stattfindet. Je höher, desto besser möchte man meinen und folgendes Diagramm scheint dies auch zu bestätigen: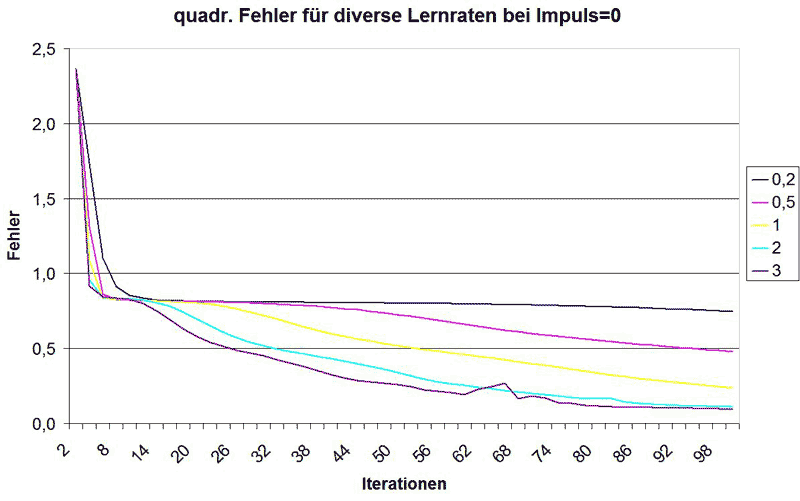
Man erkennt, dass der quadratische Fehler mit der Anzahl der Iterationen für jeden Lernfaktor-Wert stetig abnimmt. Dabei fällt E schnell, um gleich zu Beginn auf eine Art Plateau zu treffen, wo das Lernen offensichtlich nur schleppend voran geht. Hierbei kann man die Auswirkung des Lernfaktors schön sehen: bei einem Faktor von 0.2 zieht sich das Plateau sehr lang und selbst nach 100 Iterationen hat sich noch kein zufrieden stellender Wert eingestellt. Umso größer man den Lernfaktor wählt, umso kürzer wird das Plateau und umso schneller stellt sich die Konvergenz gegen 0 ein. Dies sollte bei Anwendungen, wo das Lernen zeitkritisch ist, immer oberste Priorität haben.
Die Frage ist nun: kann man den Lernfaktor beliebig stark anheben? Natürlich nicht, sonst bräuchte man eine solche Diskussion hier auch gar nicht führen. Der Grund ist einfach: wählt man einen höheren Lernfaktor, so sind die Schritte auf der Abszisse größer, mit denen man zum Minimum von E hinsteuert. Wählt man den Faktor allerdings zu groß, so wird über das Minimum von E hinaus gegangen, sodass man sich diesem nicht mehr annähert. Folgendes Diagramm zeigt bei 100 Iterationen, welche Folgen ein zu hoher Lernfaktor hat:
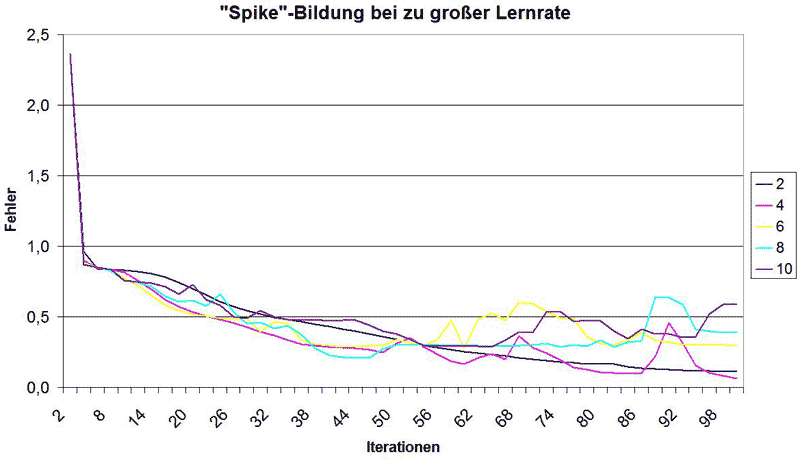
Bei einem Faktor von 2 ist die Kurve noch schön glatt, doch bereits bei 4 bilden sich "Spikes" heraus, welche die Visualisierung eines zu hohen Lernfaktors darstellen. Der Grund ist, dass über das Minimum hinaus gesprungen wurde, sich der Fehler also wieder erhöht hat. Wird sich jetzt dem Minimum von der anderen Seite angenähert, so ist nicht klar, ob dies zu einer Konvergenz gegen 0 führt. Bei 4 scheint es nach obigem Diagramm noch zu funktionieren, doch was ist mit höheren Werten? Dazu muss man sich höhere Lernraten bei mehr Iterationen anschauen, wie folgt:
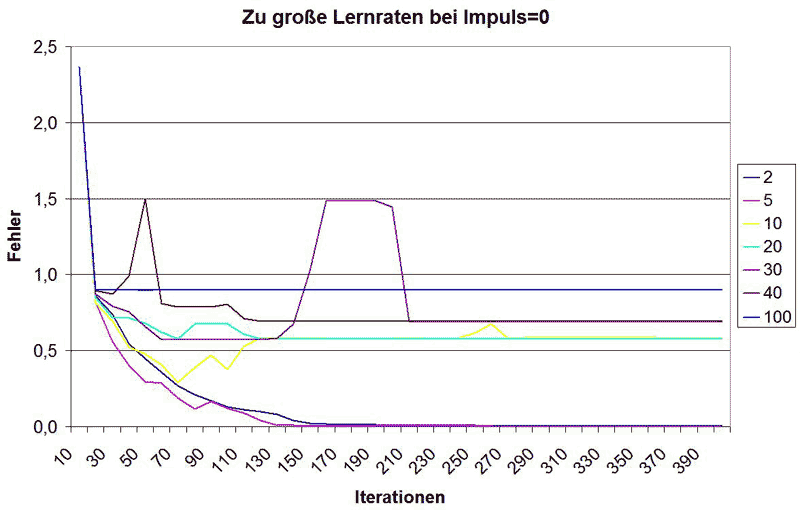
400 Iterationen reichen aus, um zu sehen, dass das ja gar nicht schön aussieht. Bei einem Lernfaktor von 2 ist noch alles gut, bei 5 hat die Funktion schon ein paar Zacken, konvergiert allerdings noch schnell, bei 10 scheint zunächst alles zu klappen, nach ca. 80 Iterationen steigt der Fehler allerdings wieder an und konvergiert gemeinsam mit der Funktion bei einer Lernrate von 20 gegen einen Fehler von ca. 0.6. Bei den Lernraten 30 und 40 konvergiert die Funktion gegen einen Wert von ca. 0.7 und bei 100 gegen 0.9 - von einem Finden des Minimums der Fehlerfunktion kann keine Rede mehr sein. Man sieht also, dass zu hohe Lernraten zu einer Konvergenz gegen eine Konstante >0 führen, was mit dem stetigen Überschreiten des Minimums der Fehlerfunktion begründet werden kann - anstatt sich diesem anzunähern, schwingen sich die Werte auf einem Fehlerwert ein, der dann nicht mehr unterschritten wird.
Das Problem der Wahl des Lernfaktors kann nicht verallgemeinernd gelöst werden. In praxi ist dies vom verwendeten Netz bzw. dessen Dimensionierung und dem Anwendungsgebiet, sprich den zu lernenden Daten abhängig. Es hat sich heraus gestellt, dass ein Lernfaktor von 2 keine Probleme bereiten dürfte, auch etwas höhere Lernraten sind denkbar und führen zu einer schnellen Konvergenz. Sollte man bestrebt sein, seine Anwendung auf Schnelligkeit beim Lernen zu trimmen, so muss man empirisch den höchsten Wert finden, für welchen das Netz noch gegen einen Fehler von 0 konvergiert und diesen Wert als Lernfaktor einsetzen.
Der Impulsterm
Auch die Wirkungsweise des Impulstermes lässt sich an obigen Gewichtsänderungsfunktionen recht gut erkennen. Zur aktuellen Gewichtsänderung wird demnach der Wert der letzten Gewichtsänderung multipliziert mit Impulsfaktor addiert. Hintergründige Überlegung dabei ist, dass bei einer starken vorherigen Änderung des Gewichtes auch die kommende Änderung hoch gewählt werden kann, da das Minimum von E noch nicht nahe ist. Dies hat zur Folge, dass die Fehlerfunktion in Abhängigkeit der Iterationen bei Wahl eines Impulsterms vor allem da steiler abfällt, wo die Funktion sowieso schon stark fällt, wie folgendes Diagramm zeigt: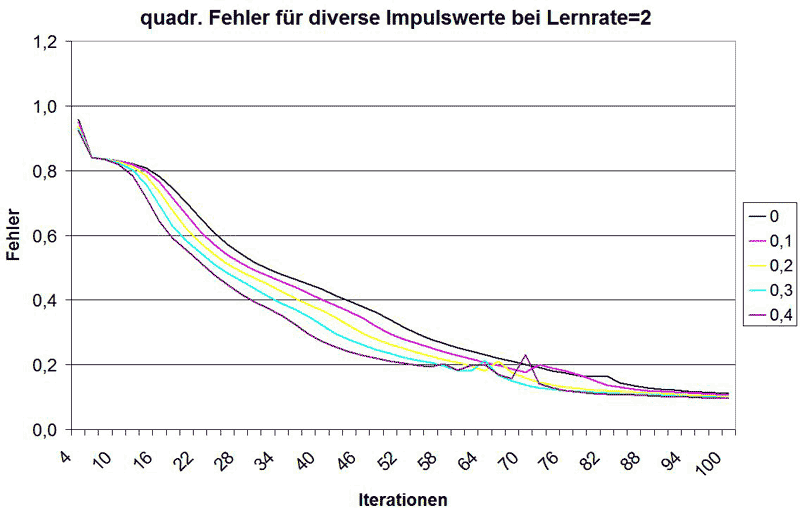
Genau wie beim Lernfaktor muss auch hier darauf geachtet werden, den Impulsfaktor nicht zu hoch zu wählen:
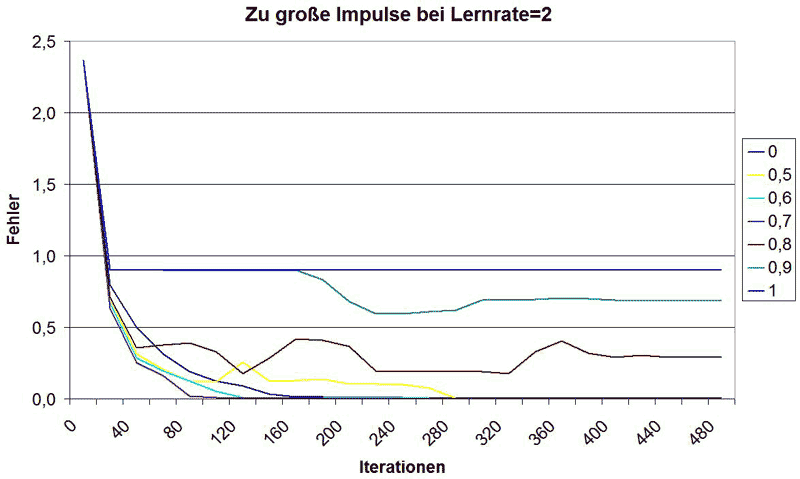
Hier passiert im Prinzip dasselbe wie beim Lernfaktor: zu hoch gewählt wird das Minimum von E überschritten und schlussendlich konvergiert die Funktion gegen einen Wert >0. Dies ist hier ab 0.8 der Fall, doch auch schon bei 0.5 verlängert sich die Konvergenzzeit anstatt sich zu verkürzen. 0.6 und 0.7 funktionieren hingegen noch außerordentlich gut, doch das ist wieder problemabhängig und kann in anderen Fällen zu nicht erwünschten Ergebnissen führen. Für mich war für dieses Problem erkennbar, dass bei einer Lernrate von 2 ein Impulsterm von 0.4 zu keinerlei Problemen geführt hat.
In Kombination
Nun ist es so, dass die optimale Wahl des Lernfaktors vom Impulsterm abhängt und andersrum. Auch hier kann man wieder empirische Untersuchungen durchführen. Z.B. habe ich den quadrierten Fehler über die Iterationen aufsummiert und ermitteln lassen, für welche Werte des Lernfaktors ein bestimmter Impulsterm zu einem optimalen Lernen geführt hat.Diese Vorgehensweise liefert folgendes Ergebnis:
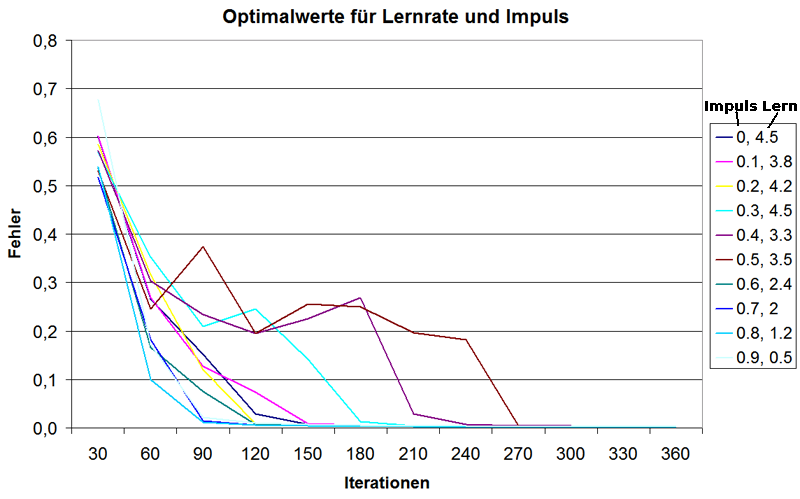
Die Impulsfaktoren 0, 0.1 und 0.2 liegen im Mittelfeld, wobei bei 0 der Lernfaktor sehr hoch gewählt werden konnte und somit sogar besser konvergiert als 0.1. 0.2 unterbietet beide...
Die besten Ergebnisse für mein Beispiel liefern allerdings die hohen Impulsfaktoren, auch wenn hier eine Lernrate von unter 3 gewählt werden musste. Dabei scheint 0.8 am besten zu konvergieren, gefolgt von 0.7 und 0.9 - per Rechnung liefert allerdings der Impuls 0.7 bei einer Lernrate von 2 den minimalsten Gesamfehler.
Hohe Lernfaktoren können sich schnell negativ auf die Konvergenz auswirken, da sie zu absolut auf die Gewichtsänderung einwirken. In praxi wird daher meist ein hoher Impulsterm (0.7-0.9) mit einem geringeren Lernfaktor (0.4-0.7) verwendet, wodurch das Minimum der Energiefunktion nicht so leicht überschritten werden kann und was dadurch selten zu Problemen führt.
Wichtig ist mir noch einmal anzumerken, dass dies nicht verallgemeinert werden kann. Andere Probleme erfordern andere Parameter und was hier funktioniert hat, kann für andere Aufgaben schon zu zuversichtlich gewählt worden sein. Daher kann ich nur davon abraten, irgendwelche hier genannten Werte blind zu übernehmen!
Fazit
Ein Neuronales Netz mit Backpropagation schneller lernen zu lassen ist kein triviales Problem, dies sollte hier klar geworden sein. Die Annäherung an ein Optimum bedarf demnach einer problemabhängigen empirischen Analyse und sollte ausgiebig getestet werden. Auch die hier genannten Werte für Lernrate und Impuls müssen nicht für jedes Problem zu einer Konvergenz gegen das Minimum von E führen, daher sollte man vorsichtig mit ihnen umgehen. Vor allem da wo es nicht unbedingt auf ein paar Sekunden ankommt, sollte man zugunsten der Stabilität lieber etwas kleinere Werte verwenden.Die von mir verwendeten Implementierungen des hier besprochenen Netzes sind hier zu finden:
C++ Klasse simpleNet
wxANN
Programm zur Auswertung von Lernrate und Impuls
Programm zur Bestimmung von Optimalwerten von Lernrate und Impuls